Area of a circle

The area of a circle is the plane region bounded by the circle's circumference.

The region shaded in gray inside of circle A above is its area.

The area of a circle can be found using the following formula:

A = πr²

where A is area, r is radius, and π is the mathematical constant approximately equal to 3.14159.

Alternatively, if using the circle's diameter, D, the area is:

Or, if using the circle's circumference, C, the area is:

Example:

Find the area of circle O below.

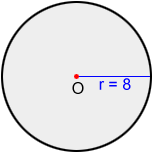
Using A = πr²,

A = π·8² = 64π ≈ 201.06

Area formula proof

The formula for the area of a circle can be proven in a number of ways. One such way involves breaking the circle into equal sectors and rearranging them to construct a parallelogram.

• In the figure above, the circle with radius r is broken into 16 sectors of equal area. Below the circle, these sectors were rearranged to resemble a parallelogram.
• The 8 arcs of the shaded sectors form the base of the parallelogram, and represent one-half of the circle's circumference, C. The height of the parallelogram is the radius, r.
• The area, A, of a parallelogram is A = bh. So, the area of our parallelogram can be approximated as .
• Since the circumference of a circle is 2πr, the area of the parallelogram is approximately .
• The higher the number of sectors we use to break up the circle, the more linear the base of the parallelogram will be. So, the exact value of the area of the circle is πr², given that an infinite number of sectors are used.