Circumference
The circumference of a circle is the distance around the boundary of the circle. The figure below shows some important parts of a circle.

- Center - The point within a circle, shown in black, that is equidistant from all points around the circle's boundary.
- Circumference - The distance around the boundary of the circle, shown in green.
- Radius - The distance from the center of the circle to any point on the boundary of the circle (shown in red).
- Diameter - The distance through the center of a circle from one side of the circle (shown in blue). It is double the distance of the radius.
What is circumference
The circumference is the perimeter of a circle or an ellipse. Generally, the perimeter is defined as the length of the curve around any closed figure. However, the term "perimeter" is conventionally used to describe the distance around the boundary of a polygon. The term "circumference" is specific to circles and ellipses.
Circumference definition
Circumference is defined as the length of the path around a circular or round shape. It is the perimeter of a curved object, rather than that of a polygon.
Circumference vs perimeter
Circumference and perimeter both measure the distance around a closed figure. The main difference between circumference and perimeter is that they are used for different types of shapes. Circumference is used for closed curved objects like circles and ellipses. Perimeter is used for polygons, or closed objects with straight rather than curved edges.
Generally, perimeter could be used to describe the distance around a circle. On the other hand, circumference cannot be used to describe the distance around a polygon. This is clear in the definition of circumference, since the distance can be described as the perimeter of the circle. However, we cannot say "the circumference of a square," since circumference is intended specifically for use with curved figures, while perimeter is mainly conventionally used to describe this distance around a polygon.
How to find circumference
To find the circumference of a circle, there are a few different formulas.
Circumference formula
The formula for circumference is based on the constant π (pi), which is an irrational number approximately equal to 3.14159. π is the ratio of the circumference to the diameter of any circle.
Circumference formula using diameter
Since π = C/d, where C is circumference and d is diameter, we can derive the circumference formula as follows:
Circumference formula using radius
Since the diameter (d) is two times the radius (r), another circumference formula is:
Circumference formula using area
The circumference of a circle can also be found if the area (A) of the circle is known using the circumference formula:
Below are some circumference examples.
Examples:
1. What is the circumference of a circle with radius 4.4?
Since we are given the radius, we can use C = 2πr to get
C = 2π(4.4) = 8.8π ≈ 27.646
2. A circle has an area of 100π. What is the circle’s circumference?
Using the formula ,
Circle formulas
Using the above formulas and the area of a circle formula, we can convert between the various measurements of a circle.
Circumference to diameter
To find the diameter using circumference, divide the circumference by π:
Circumference from diameter
To find the circumference from the diameter, multiply the diameter by π:
Circumference to area
To find the area of a circle from the circumference, first divide by 2π to get the radius:
Then, square the radius and multiply by π to find the area of the circle:
Circumference from area
To find circumference from area, first find the radius by dividing area by π, then taking the square root of the result:
Then, multiply the radius by 2π to find circumference:
Circumference to radius
To find the radius using circumference, divide the circumference by 2π:
Circumference from radius
To find the circumference from radius, multiply the radius by 2π:
How to measure circumference
To measure circumference in real life, use the following steps.
- Use a long object such as string or thread to trace around the boundary of the entire circle. Start at one end of the string and trace the circle until the end meets the other part of the string.
- Mark or cut the string where the end meets the other part of the string.
- Straighten the string and use a straightedge, ruler, measuring tape or some other measurement tool to measure from the end of the string to the mark on the string (or where you cut it). This length is the circumference of the circle.
Being able to measure circumference is useful for everyday applications such as body measurements (chest, hips, arms, legs, etc.) for clothing, measuring distances like that around a track, measuring the sizes of circular objects or decorations for your living space, and more.
Circumference of an ellipse
A circle is a special case of an ellipse where the minor and major axes (a and b in the figure below) are equal. To find the circumference of an ellipse, use the following formula:
where C is the circumference, and a and b are the lengths of the semi-axes of the ellipse. This equation is just an estimation because a more exact formula requires the use of non-elementary functions.
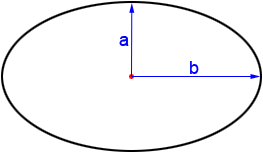
If we were to plug in equal values for a and b, say r, we would get the equation for the circumference of a circle:
| C = | |
| = | |
| = | 2πr |
