Circle
The set of all points in a plane that are equidistant from a fixed point, defined as the center, is called a circle.
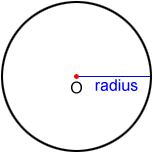
The circle above is called circle O. A line segment with two endpoints, one on the center and the other on the perimeter of the circle, forms a radius, r, of the circle.
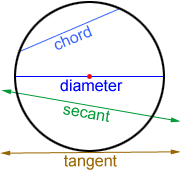
A chord is a line segment whose endpoints lie on the perimeter of the circle. If the chord contains the center, it is called a diameter of the circle. The diameter is twice the length of the radius.
A line is called a secant line if it intersects the circle at two points. A line is called a tangent line if it intersects the circle at only one point, called a point of tangency.
Circles are widely studied in geometry. The following are some important concepts related to circles.
Circumference
The circumference, C, of a circle is similar to the perimeter of a polygon in that it is a measure of the distance around the circle.
The circumference of circle above can be found using the formula
C = 2πr
where r is the circle's radius. You can also use the formula C = πd, where d is the diameter of the circle. π is a mathematical constant that represents the ratio of the circle's circumference to its diameter. It is approximately equal to 3.14.
Example:
The figure below shows circle A with radius AB = 4.4 that has a circumference
C = 2π·4.4 = 27.6.
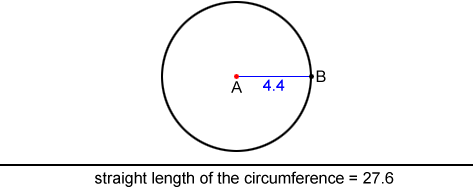
The line segment below the circle represents the straight length of its circumference.
Arc of a circle
An arc of a circle is part of a circle.
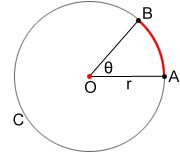
Arc AB, written symbolically as , is shown in red for circle O.
is called a minor arc since it encompasses less than one-half the circles circumference.
is called a major arc since it encompasses more than one-half the circle's circumference. Minor arcs are usually named using two points while major arcs are usually named using three.
An arc's length is a portion of the length of the circumference of a circle. It can be calculated by using the formula,
where θ is the central angle, in units of degrees, subtended by the arc. If the angle is given in radians, the arc length can be found using:
s = rθ
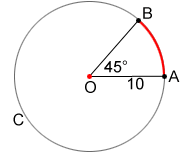
For circle O below, the measure of is,
Area
The area of a circle is the plane region bounded by the circle's circumference. Area is measured in square units of length while circumference is measured units of length.
The region shaded in gray inside of circle O above is its area. The formula for the area is
A = πr2
where r is the circle's radius.
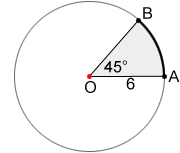
Sector
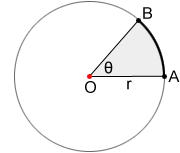
A sector of a circle is the enclosed region bounded by two radii and the arc they form. Sector OAB below, formed by radii OA, OB, and , is the gray region of circle O.
The area, A, of a sector can be calculated by using the formula,
where θ is the central angle (in degrees) that forms the sector. If the angle is given in radians, the area of the sector can be found using:
For circle O below, the area of sector OAB is,
Alternatively, the area of a sector can be found using the formula,
where r is the radius and s is the sector's arc length.
Did you know?
The region between two concentric circles is called an annulus. The name comes from a Latin root meaning "little ring." The term "annulus" is also used to name ring-like structures such as the yearly growth ring of a tree:

