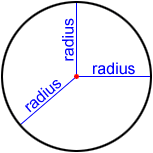
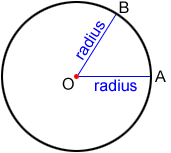
Radius
The radius (plural radii) of a circle is any line segment that has one endpoint on the center of the circle and the other endpoint on the circle's circumference. It can also be defined as the distance from the center of a circle to a point on its circumference. A circle contains infinitely many radii.
The spokes on the wheel of a bicycle wheel are radii of its circular rim.
Radius and diameter
The radius of a circle is one-half the length of its diameter.
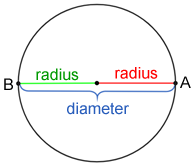
The two radii of length r, shown above for the circle, lie on its diameter, d. This means that d = 2r or .
Central angles
A central angle is formed by two radii of a circle.
Radius of a polygon
A radius of a regular polygon is the radius of its circumcircle, which is a circle that intersects each vertex of the polygon. A radius for a regular pentagon is referred to as a circumradius.
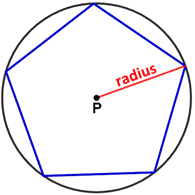
Circumcircle P of the regular pentagon above has 5 radii, each of which are formed by a line segment that has one endpoint on point P and the other on one of the 5 vertices of the pentagon.
Radius as an angle unit
In the study of Trigonometry, the radius of a circle is used to measure an angle with a unit of measure called a radian. If the length of an arc is equal to the length of the radius, the central angle subtended by the arc is 1 radius unit, or 1 radian. Generally, the measure of an angle in radians is some multiple of the length of the radius.
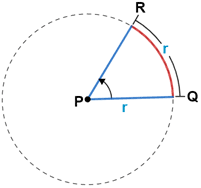
For central angle QPR above, the measure of arc QR is equal to the length of the radius, so ∠QPR = 1 radian.
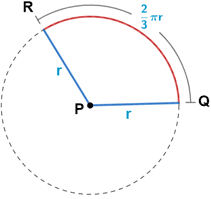
For central angle QPR above, the measure of arc QR is or about 2.1 times the radius, so
radians.
Radius of a sphere
The radius of a sphere is any line segment from the center of the sphere to a point on the sphere. A sphere has infinitely many radii, but only three radii are shown in the sphere below as examples:
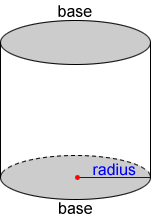
Radius of a cylinder
The bases of a right circular cylinder are circles. The radius of one of the circular bases is also the radius of the cylinder, as shown below.