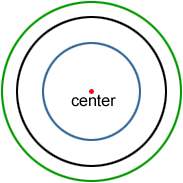
Concentric circles
Concentric circles are circles that share the same center. A pebble dropped in a pond creates concentric circles. So do the ripples formed by a milk drop shown below.

If two or more circles are concentric in the same plane, they must have different radii. Concentric circles will never intersect, and the distance between any two concentric circles is the same all the way around.
The area of the region between two concentric circles in the same plane is called the annulus.
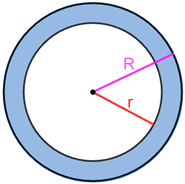
The area of an annulus can be calculated with the formula:
A = π(R2 - r2)
Where R is the radius of the outer circle and r is the radius of the inner circle.
Example:
What is the area of the annulus of two concentric circles given that the circles have a radius of 4 and 7?
A = π(R2 - r2)
A = π(72 - 42) = 33π ≈ 103.67
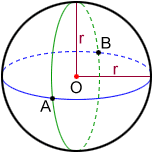
Concentric circles in 3D
For two or more circles to be concentric, the circles must be different circles. Therefore, in 2D, two concentric circles must have radii of different lengths and cannot intersect. In 3D, however, it is possible for two distinct circles to share the same center, have the same radius, and intersect.
For sphere O below, the two great circles in blue and green are concentric circles. They both have the same center at point O, a radius of r, and they intersect with each other.