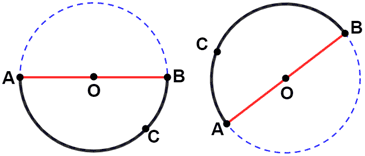
Semicircle
A semicircle is half of a circle. It resembles a round paper plate folded in half.

An arc on a circle that has endpoints that lie on a diameter of the circle is a semicircle.
Perimeter of a semicircle
To find the perimeter of a semicircle, we need to know either the diameter or radius of the circle, as well as the arc length of the semicircle. The arc length of the semicircle can be thought of as half the circumference of the circle. Since the circumference of a circle is C = πd or C = 2πr, where C is the circumference, d is the diameter, and r is the radius, dividing these equations by 2 gives us the equations for the arc length of the semicircle:
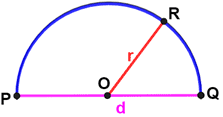
Adding the diameter of the circle to the equation gives us the equations for the perimeter of a semicircle:
where P is the perimeter, d is the diameter, and r is the radius of the semicircle.
Area of a semicircle
Since a semicircle is half a circle, we can derive its area equation by dividing the equation for the area of a circle by 2:
where A is the area and r is the radius of the semicircle.
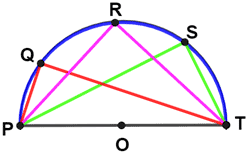
Inscribed angles of a semicircle
An inscribed angle of a semicircle is any angle formed by drawing a line from each endpoint of the diameter to the same point on the semicircle, as shown in the figure below. An inscribed angle has a measure that is one-half the measure of the arc that subtends it. Since a semicircle is half of a circle, the angle subtended by the arc that forms the semicircle measures 180°. Therefore, any inscribed angle of a semicircle is 180°/2 = 90°; they are all right angles.