Binomial distribution
A binomial distribution is a type of discrete probability distribution that results from a trial in which there are only two mutually exclusive outcomes. These outcomes are labeled as a success or a failure.
The binomial distribution is commonly used to determine the probability of a certain number of successes in n trials, where the probability of success on a single trial does not change. One such example is the flip of a coin. The two possible outcomes of a coin flip are heads or tails, and the probability of heads or tails occurring is the same for each trial (50% for a fair coin). Thus, the flip of a coin meets the conditions of a binomial distribution, and probabilities such as the probability of 3 heads occurring in 5 flips of a coin can be determined.
In summary, for an event to exhibit a binomial distribution, the following conditions must be met:
- The trials are independent, so the outcome of any one trial has no bearing on the outcome of another.
- Each trial has only two outcomes, labeled success or failure, where the probability of success is p and the probability of failure is q = 1 - p.
- The probabilities of success and failure are constant for each successive trial. If p = 0.6, then q = 0.4 for every trial.
- The outcomes of a trial are mutually exclusive (they cannot both occur at the same time). A coin cannot both land on heads and tails.
The probability mass function (pmf) of a binomial distribution is:
, where
| p is the probability of success |
| q = 1 - p is the probability of failure |
| n is the number of trials |
| x is the number of successes from the n trials |
Thus, if X is a discrete random variable that exhibits a binomial distribution, the probability, P(X = x) = f(x), where f(x) is defined as above.
Example
A fair 6-sided die is rolled 4 times. Using a binomial distribution,
- find the probability of rolling a 6 three times.
- find the probability of rolling a 6 at least two times.
i. Rolling a 6 is a success in this case. Rolling anything else is a failure. Thus, p = 1/6 and q = 5/6. There are 4 trials, and we want to determine the probability of 3 successes, or x = 3. Thus:
Thus, there is about a 1.5% chance of rolling a 6 three times in 4 trials.
ii. Rolling a 6 at least two times means that we can roll a 6 twice, three times, or four times. The probability of rolling a 6 at least two times is the sum of the probabilities of rolling a 6 two, three, or four times.
Thus, there is a 13% probability of rolling a 6 at least 2 times in 4 rolls.
Mean and variance
The mean (or expected value), μ, and variance, σ2, of a binomially distributed random variable can be found using the following formulas:
Example
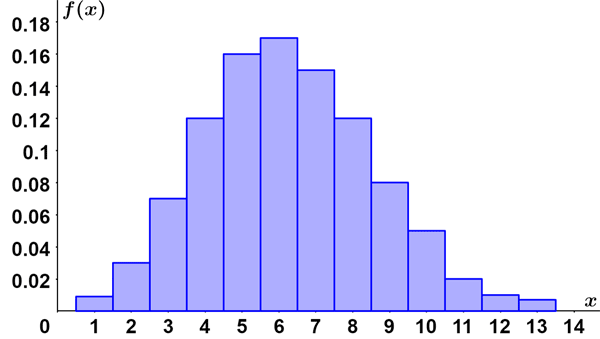
200 ping pong balls of various colors are placed in a bin. 25 of the ping pong balls are red.
- Find the probability of selecting a red ball on any single draw given that the selected ball is replaced prior to each subsequent selection.
- Find the expected value and variance given that 50 balls are randomly selected (with replacement) from the bin.
- Find the probability of selecting 6 red balls from the 50 balls that were randomly selected from the bin.
i. There are 25 red balls and a total of 200 balls, so:
p = 25/200 = 1/8
ii. n = 50 and p = 1/8, so:
μ = np = 50 × 1/8 = 6.25
Thus, we would expect around 6 of the selected ping pong balls to be red. The variance is computed as:
σ2 = 50 × 1/8 × 7/8 = 5.47
iii. The experiment meets the criteria of a binomial distribution, so:
Thus, while we would expect to choose 6 red balls from the 50, the probability of doing so is only 17%. The binomial distribution for this experiment is shown in the figure below: