Covariance
Covariance is a measure of the linear association between two random variables; it measures the degree to which variation in one random variable matches the variation of another variable.
- Positive covariance - variables that exhibit positive covariance tend to move in the same direction: the greater values of one variable tend to correspond to the greater values of the other and the lesser values of one variable tend to correspond to the lesser values of the other.
- Negative covariance - variables that exhibit negative covariance tend to move in opposite directions (have an inverse relationship): the greater values of one variable tend to correspond to the lesser values of the other.
- Covariance of 0 - variables that have no linear tendency have a covariance of 0. Two independent variables would therefore have a covariance of 0. The opposite is not always true; having a covariance of 0 does not necessarily indicate that the variables are independent (the variables can still be dependent).
| Positive covariance | Negative covariance | Zero covariance |
|---|---|---|
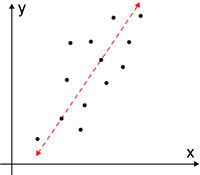
|
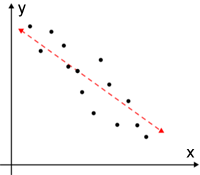
|
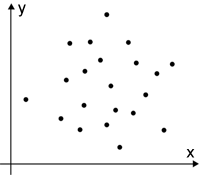
|
Covariance only indicates the direction of the relationship between two variables. The magnitude of the covariance does not really provide information about the strength of the relationship (i.e. higher covariance doesn't mean a stronger relationship). This is because covariance is not normalized, so the magnitudes of the variables affect the magnitude of the covariance (covariance values can range from -∞ to ∞).
To determine the strength of the linear relationship between two random variables, covariance can be normalized by the variance of each variable to find their correlation, a value that ranges between -1 and 1. A correlation of -1 or 1 indicates a perfect negative or positive correlation, respectively, and a correlation of 0 indicates no correlation.
Covariance formulas
Different formulas are used to compute the covariance depending on whether the available data is derived from a sample or the entire population.
Population covariance
The population covariance formula is used when population data is available, meaning that data is available for the entire group being studied rather than just a sample of the population:
| xi is an element of the random variable x |
| yi is an element of the random variable y |
| μx is the population mean for the random variable x |
| μy is the population mean for the random variable y |
| N is the size of the population |
Sample covariance
In many cases, it is not feasible to collect data from an entire population, so sampling methods are used instead to collect data from a sample of the population. Thus, many statistical measures (including covariance) have separate formulas depending on whether the data being interpreted is derived from a sample of the population or the entire population:
| xi is an element of the random variable x |
| yi is an element of the random variable y |
| x is the sample mean for the random variable x |
| y is the sample mean for the random variable y |
| n is the size of the sample |
In most cases, covariance is calculated using a computer or calculator, since there are usually too many data points to compute covariance by hand. Just to demonstrate the use of the formula, a worked example is shown below.
Example
Find the covariance given a sample of the heights and weights of men who frequent a particular gym:
| x = height (in) | y = weight (lbs) |
|---|---|
| 63 | 170 |
| 67 | 175 |
| 69 | 177 |
| 72 | 190 |
| 73 | 184 |
The sample means are calculated as follows:
The table below shows the intermediary values in the computation of covariance:
| (xi - x) | (yi - y) | (xi - x)(yi - y) |
|---|---|---|
| 63 - 69 = -6 | 170 - 179 = -9 | (-6)(-9) = 54 |
| 67 - 69 = -2 | 175 - 179 = -4 | (-2)(-4) = 8 |
| 69 - 69 = 0 | 177 - 179 = -2 | (0)(-2) = 0 |
| 72 - 69 = 3 | 190 - 179 = 11 | (3)(11) = 33 |
| 73 - 69 = 4 | 184 - 179 = 5 | (4)(5) = 20 |
Thus, the sum of the product of the differences is
and the covariance is:
Since the covariance is positive, the data indicates that larger heights tend to correspond to larger weights.
