Degrees to radians
Degree and radian are two of the most common units of measurement for angles. To convert from degrees to radians, multiply an angle in degrees by or use the converter below.
Example:
Convert 90° to radians:
While many different units have been used to measure angles throughout history, radians and degrees are the most common angle measures used today.
Below are two angles that have the same measure. The one on the left is measured in radians and the one on the right is measured in degrees.

Relationship between degrees and radians
We can derive the relationship between degrees and radians based on one full rotation around a circle. One full rotation around a circle is equal to 360°. The measure of a radian is equal to the length of the arc that subtends it divided by the radius, or
where θ is the angle in radians, s is the arc length, and r is the radius of the circle. The circumference, c, of a circle is measured as
c = 2πr
where r is the radius. The length of the arc that subtends the central angle of a circle in the case of a full rotation is equal to the circumference of the circle. Thus, s=c=2πr. Substituting this into the equation for radian measure,
In the figure below, the blue ray indicates the terminal side of the angle whose initial side is the positive x-axis. The circular black arrow indicates the measure of a full rotation in degrees, and the angle measure in radians is shown in red.
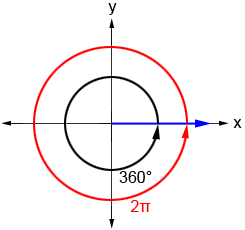
Based on this, the relationship between radians and degrees is:
| 2π radians = 360° |
| π radians = 180° |
Therefore:
Commonly used angles in trigonometry
While the conversions above can be used to convert between any radian or degree measure, there are a number of angles in trigonometry that are so frequently used that it is worth memorizing their measures. These angles are shown in the circle below.
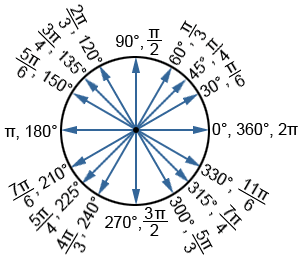
It is also common for the sines and cosines of these angles on a unit circle to be listed. Refer to the respective pages for more detail.
