Degree
A degree is a unit of measure, denoted by the symbol °, used to indicate the measure an angle in a plane. An angle measuring 1°, read 1 degree, is equal to of one complete revolution of the angle about its vertex. You can see from the diagram below that the counterclockwise rotation of the terminal side of an angle forms a circular path for the angle.
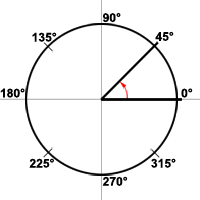
One full rotation is equivalent to 360°. One-quarter of a turn produces an angle that measures 90°, and one-half of a rotation creates an angle of 180°. While angles can have measures greater than what is shown, by doing multiple rotations, we will mostly only look at angle measures up to 360° in the study of Geometry.
Did you know?
Angles can have other units of measure too. Angles can be measured in radians, which compares the arc length produced by the rotation of an angle with the radius of the circle. An angle that measures 180° has a measure of π radians. Another unit of measure for an angle is called the slope. It may also be called grade, incline, gradient, mainfall, pitch or rise. The slope of an angle measures the ratio of the vertical distance over the horizontal distance at the terminal end of the angle. Slope is often represented as a percentage. You may have experience with this unit of measure from climbing or driving up a mountain. The steepness of a hill or mountain is often described in terms of slope, or grade. For example, a hill may have a 5% grade.
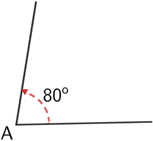
When using the degree symbol be careful not to use it for the name of an angle, only its measure.
The name of the angle shown below is ∠A not ∠A°. When stating its measure, use m∠A = 80° or simply ∠A = 80° where ∠ is the symbol used to denote an angle.
Special angles
Some angles are used more often in Geometry due to their measures:
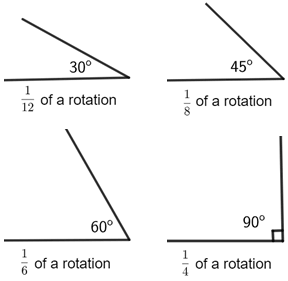
Notice the 90° angle has a small square at its vertex. This notation indicates an angle that measures 90° and it is not necessary to state the angle's measure numerically.
Measuring angles
A protractor is a common tool used to measure angles. Most protractors measure angles in degrees.
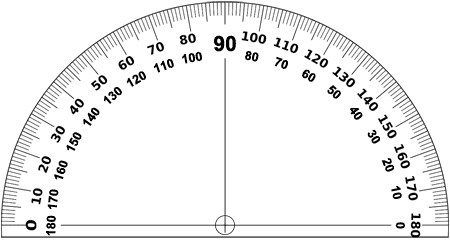
Protractors usually have two sets of numbers. Both sets can be used to measure an angle in degrees. The outside set goes from 0 to 180 degrees where the 0 is on the left side of the protractor. The inner set goes from 180 to 0 degrees where 0 is on the right side of the protractor. Whichever side you line up with the zero-degree line determines which set of numbers to use. See how to measure an angle in degrees using a protractor here.
Did you know?
Angles that have a decimal degree measure such as 15.66° can be converted to a unit of measure in degrees-minutes-seconds where the decimal portion of the degree measure is expressed in minutes and seconds. 1° = 60' = 3600" where the ' symbol represents minutes and " represents seconds. So, 15.66° = 15°39'36" which is read as 15 degrees 39 minutes 36 seconds.
