Radian

A radian (sometimes indicated as "rad") is a unit of measurement for angles. It is used in many areas of mathematics, such as trigonometry, calculus and, more.

Radian definition

A radian is a measurement of angle based on the radius of a circle. 1 radian is the angle that is subtended by an arc that has a length equal to the radius of the circle. In the figure below, θ=1 radian.

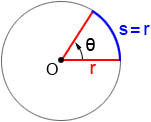
The radian measure of any central angle (angle whose vertex is at the center of a circle) is equal to the length of the intercepted arc divided by the radius, or radians, where θ is the angle in radians, s is the arc length, and r is the radius.

As a ratio of two lengths, radians are commonly considered a "pure number," meaning that it is dimensionless. Thus, "rad" is very rarely used to indicate that an angle measure is in radians. Rather than writing "1 rad," a radian is most typically written as simply "1" and an angle measure that doesn't specify some other unit is assumed to be in radians.

Radian v.s degree

Degree is another unit of measure for angles, denoted by the symbol °. An angle measuring 1° is equal to of one complete revolution of the angle about its vertex.

To convert from radians to degrees, or degrees to radians, use the following conversions:

Thus, to convert a measure that is in degrees to radians, multiply by . To convert an angle in radians to degrees, multiply by .

When using degrees, a degree (°) symbol is used to indicate that the angle is not in radians.

1 radian ≈ 57.296°

Radians in a full circle

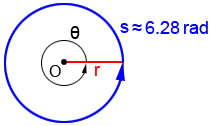
The circumference of a circle is 2πr where r is the radius of the circle. Since the circumference of a circle encompasses one complete revolution of the circle, its arc length is s = 2πr. Plugging this into the formula for radian measure,

and 2π ≈ 6.28, so there are approximately 6.28 radians in a circle:

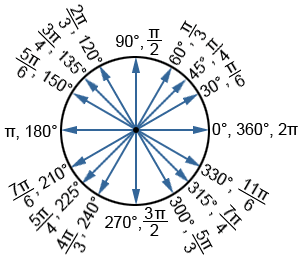
Commonly used angles in radians

We can use the fact that 1 complete revolution equals 2πr to find angle measures in radians and degrees that are commonly used in the study of trigonometry.

1 revolution = 2π rad = 360°

of a revolution = π rad = 180°

of a revolution = π rad = 120°

of a revolution = π rad = 90°

of a revolution = π rad = 60°

of a revolution = π rad = 45°

of a revolution = π rad = 30°

Below is a list of angles on a circle measured in degrees and radians that are commonly used in trigonometry.