Line
A line is a collection of points along a straight path extending indefinitely in both directions. This is indicated by the arrows at each end, shown in the figure below.
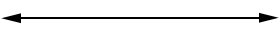
A line has one dimension, its length. Two non-overlapping points determine a unique line and we can name the line with those two points or any other two points on the line.
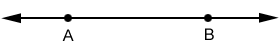
line or defined by points A and B
Lines are used in shapes, angles, and many other geometric contexts.
Lines and angles
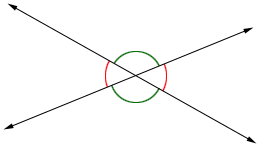
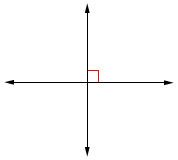
When two non-overlapping lines intersect at a point, two pairs of vertical angles are formed.
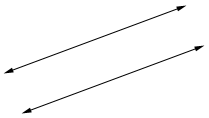
When 2 non-overlapping lines never intersect, they are called parallel lines.
When 2 lines intersect at a right angle, we say the lines are perpendicular to each other.
Lines and planes
Lines and polygons
Three or more intersecting lines can form a polygon whose vertices are the points at which the lines intersect.
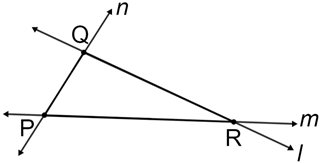
Line l, m, n above intersect at points P, Q, and R forming triangle PQR. Also, P, Q, R are the vertices for the triangle formed.
Determination of planes
A plane can be determined in a number of ways:
- Three points that are not on a single line can determine a plane
- A line and a point that is not on the line can determine a plane
- Two non-overlapping parallel lines determine a plane
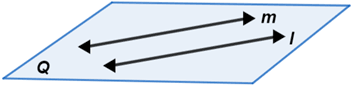
- Two intersecting lines determine a plane
Properties of planes
- Relative to a plane, a line can only be parallel to the plane, intersect it at a single point, or be contained in the plane (intersect it at all points)
- A line divides a plane into two equal parts (since a plane extends indefinitely too).
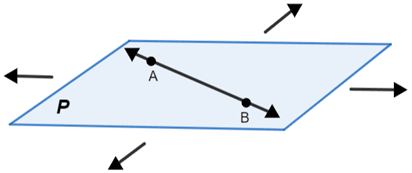
Line lies on plane P and divides it into two equal regions. - Two planes can only either be parallel, or intersect along a line
- If two planes intersect, their intersection is a line.
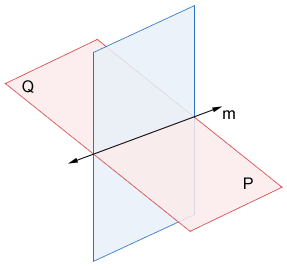
Planes P and Q intersect at line m. - If two lines are perpendicular to the same plane, the two lines must be parallel (as long as they are not the same line)
- If two planes are perpendicular to the same line, the two planes must be parallel (as long as they are not the same plane)
