Polyhedron
In Geometry, a polyhedron (plural: polyhedra) is a closed space figure whose faces are polygons. The word polyhedron has Greek origins, meaning many faces. Below are a few polyhedron examples.

|

|

|
| Hexagonal prism | Tetrahedron | Cube |
What is a polyhedron
A polyhedron is a three-dimensional (3D) solid figure that is made up of only polygons, meaning that the figure has no curves. Real world examples of polyhedra include the Great Pyramid of Giza, concrete blocks, dice, bricks, and more.
Polyhedron parts
Polyhedrons are made up of faces, edges, and vertices. They are named based on the number of faces they have. For example, a tetrahedron has 4 faces, a pentahedron has 5 faces, and a hexahedron has 6 faces.
- Faces: the polygons that form the polyhedron. Polyhedrons typically have 1 or 2 faces that are also referred to as bases.
- Edges: the line segments created by two intersecting faces.
- Vertices: points where three or more edges meet.
For example, a hexagonal prism has 8 faces (6 lateral and 2 bases), 18 edges, and 12 vertices.

There is a theorem that relates the faces, edges, and vertices of a polyhedron. Using this theorem, it is possible to determine the number of faces, edges, and vertices of a polyhedron given you know the number of at least two of them.
Euler's Theorem - Faces, edges, vertices
Euler's Theorem relates the number of faces, vertices, and edges of a polyhedron. It states that the sum of the faces and vertices minus the number of edges always equals two:
F + V - E = 2
where F is the number of faces, V is the number of vertices, and E is the number of edges of a polyhedron.
Example:
For the hexagonal prism shown above, F = 8 (six lateral faces + two bases), V = 12, and E = 18:
8 + 12 - 18 = 2
Types of polyhedron
Polyhedrons typically fall into three groups: Platonic solids, prisms, and pyramids. They can further be categorized as regular or irregular and convex or concave. A regular polyhedron is a polyhedron whose faces are all congruent regular polygons; any polyhedron that does not meet these conditions is considered irregular. Only the Platonic solids are regular polyhedra; prisms and pyramids are irregular polyhedra.
Platonic solids
A Platonic solid, also referred to as a regular polyhedron, is a polyhedron whose faces are all congruent regular polygons. In a Platonic solid, the same number of faces meet at each vertex. There are only 5 Platonic solids, and their names indicate the number of faces they have. The 5 Platonic solids are the tetrahedron, cube, octahedron, dodecahedron, and icosahedron. The figure below shows these shapes as well as the polyhedron net for each.
The 5 Platonic solids
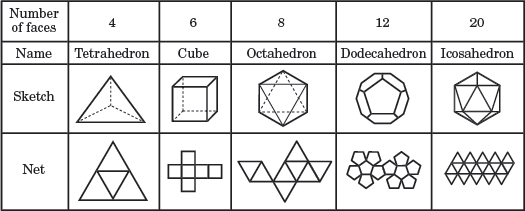
A polyhedron net is a 2D pattern of polygons that can be modified to form each polyhedron.
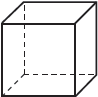
Most regular prisms are generally not considered regular polyhedra. A cube is the only regular prism that can also be classified as a regular polyhedron.
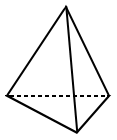
Likewise, a regular tetrahedron is the only regular pyramid that is also a regular polyhedron.
Prisms
Prisms are polyhedra that have two congruent faces, called bases, lying in parallel planes. A prism is typically named by the shape of its polygonal bases. The lateral faces (the sides that are not bases) are parallelograms, rectangles, or squares.
| Regular prism | Irregular prism |
|---|---|
 |
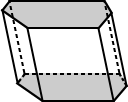 |
| The bases for the regular hexagonal prism above have bases that are regular hexagons. | The bases for the hexagonal prism above are irregular hexagons. |
Pyramids
Pyramids are polyhedra that have polygons as bases and triangles as all other faces. A pyramid is typically named by the shape of its polygonal base.
| Regular pyramid | Irregular pyramid |
|---|---|
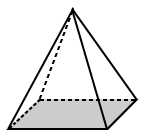 |
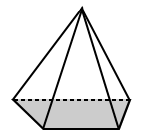 |
| The base of the square pyramid above has a base that is a square (a regular polygon). | The base for the trapezoidal pyramid above is a trapezoid with unequal sides (so it is an irregular polygon). |
Concave polyhedron
A concave polyhedron has at least one face that is a concave polygon. For a polyhedron to be classified as concave, it must be possible to draw a line segment between two points such that the line segment goes outside the polyhedron.

In the polyhedron above, line segment AB is outside of the polyhedron, making it a concave polyhedron. As long as a line segment can be drawn anywhere between two points on the surface of the polyhedron, the polyhedron is classified as concave.
Convex polyhedron
A convex polyhedron is a polyhedron in which a line segment cannot be drawn between two points such that the segment goes outside the polyhedron.

In the polyhedron above, line segment AB is inside of the polyhedron, and there is no way to draw any line segment between two points on the surface of the polyhedron such that the line segment will be outside of the polyhedron. For this reason, the polyhedron above is classified as a convex polyhedron.
Irregular polyhedron
An irregular polyhedron is a polyhedron in which the faces are not all congruent regular polygons, or different numbers of faces meet at each vertex. All Platonic solids are regular polyhedra and any polyhedron that is not a Platonic solid is an irregular polyhedron. There are very few regular polyhedra (only 5). Most polyhedra are irregular, including all prisms and pyramids, which are two of the most common groups of polyhedra.
Polyhedron formulas
Aside from Euler's Theorem above, other polyhedron formulas like surface area and volume are dependent on the type of polyhedron.
Surface area of a polyhedron
The surface area of a polyhedron is found by finding the area of each of the faces of the polyhedron. For a triangular pyramid, the surface area is the sum of the areas of each of the triangles that form the pyramid. If the base of the pyramid is rectangular, the surface area is the sum of the area of the rectangle and the four other triangles. For example, given a regular tetrahedron, which is made up of 4 equilateral triangles, the surface area of the tetrahedron is:
SA = 4 × ½ bh = 2bh
Although the surface area formula is different for all polyhedrons, the format is more or less the same. Just find the areas of each individual face. The surface area of a Platonic solid will be nA, where A is the area of a face and n is the number of faces in the Platonic solid.
| Platonic solid | Surface area* |
|---|---|
| Tetrahedron | |
| Cube | |
| Octahedron | |
| Dodecahedron | |
| Icosahedron | |
| *a is the length of a side | |
Volume of a polyhedron
The volume of a polyhedron is dependent on the type of polyhedron.
Volume of a Platonic solid
The volume of the Platonic solids formulas are as follows:
| Platonic solid | Volume* |
|---|---|
| Tetrahedron | |
| Cube | |
| Octahedron | |
| Dodecahedron | |
| Icosahedron | |
| *a is the length of a side | |
Prism volume
The volume of a prism is the area of the base multiplied by the height of the prism. This is because a prism is made up of two congruent polygonal bases. Thus, the general volume of a prism formula is:
V = Bh
where B is the area of the base and h is height. For example, if the base is a square, B = s2 where s is a side of the square, multiplied by the height of the polyhedron. If the base is a triangle, B = 1/2bh, where b is the base of the triangle and h is its height, and so on.
Pyramid volume
The volume of a pyramid is ⅓ the area of the base of the pyramid multiplied by the height of the pyramid. The general volume of a pyramid formula is:
V = ⅓Bh
where B is the area of the base and h is the height of the pyramid.
