Rectangle
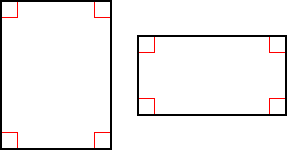
A rectangle is a quadrilateral with four right angles. The following are two examples.
Rectangles are one of the most common shapes you will see in daily life. Many objects around us are rectangular in shape, such as a book, a phone, a door, a card, and many more.
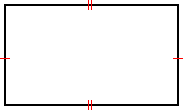
Sides of a rectangle
The opposite sides of a rectangle are congruent and parallel to each other. The longer sides of a rectangle are typically referred to as its length while the shorter sides are referred to as its width.
Angles of a rectangle
A rectangle contains four interior right angles. Angles A, B, C and D equal 90° in the rectangle shown below.

Diagonals of a rectangle
There are two diagonals in a rectangle. The two diagonals ( and in the rectangle below) are congruent and bisect each other. Each diagonal divides the rectangle into two congruent right triangles.
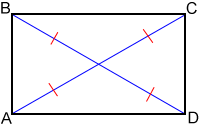
Diagonal divides rectangle ABCD into triangles ABD and CDB. ≅ and ≅ since opposite sides of a rectangle are congruent. ∠A≅∠C since the interior angles of a rectangle are right angles. Therefore, △ABD≅△CDB by the Side-Angle-Side postulate.
Square
A square has four congruent sides and four right angles, so it is also a rectangle. A rectangle is a square when all of its sides are congruent.
Symmetry in a rectangle
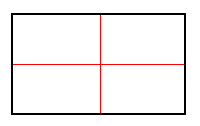
A rectangle has 2 lines of symmetry and a rotational symmetry of order 2, which means that it can be rotated in such a way that it will look the same as the original shape 2 times in 360°.
| Lines of symmetry | Rotational symmetry |
|---|---|
 |
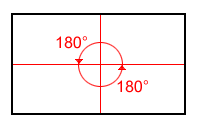 |
| 2 lines of symmetry | two 180° angles of rotation |
Area of a rectangle
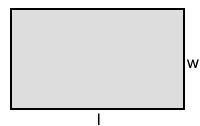
The area of a rectangle is the product of its length and width.
A = l·w
Where l is the length and w is the width of the rectangle. Some textbooks might write the dimensions of a rectangle as base and height instead of length and width.
Did you know?
A golden rectangle is a rectangle in which the ratio of its length to its width is the golden ratio. For the rectangle below with a length of (a + b) and width of a, =φ, where φ is the golden ratio and is equal to approximately 1.618. The rectangle shown below in purple also satisfies the golden ratio:
=φ.

