Vertex

A vertex (vertices for plural) is a point at which two or more sides or edges of a geometric figure meet.

Vertex of an angle

The vertex of an angle is the common endpoint of two rays that make up the angle's sides.

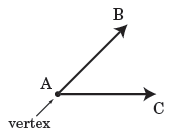
The vertex for angle BAC, written ∠BAC, is point A. The angle can also be named as ∠CAB or by only its vertex, ∠A. When using three points to name the angle, always put the name of the vertex in the middle. So, ∠BAC is not the same angle as ∠ABC or ∠BCA.

Be careful when naming an angle that shares a common vertex with other angles.

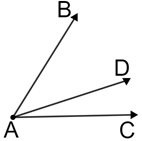
∠BAC above cannot be named by only its vertex since angles ∠CAD and ∠BAD both have A as their vertex. In this case each angle must be named by the points on each side making up the angle and the angle's vertex.

Vertex of a polygon

The vertex of a polygon is a point at which two sides of the polygon intersect. The vertices are also referred to as corners of the polygon. In any polygon, the number of vertices is equal to the number of sides of the polygon. The figure below shows a rectangle. Since rectangles have 4 sides, they also have 4 vertices. The vertices of the rectangle are points A, B, C, and D.

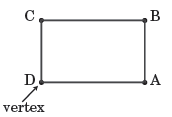
Naming polygons by their vertices

Polygons can be named by their vertices as long as they are listed in consecutive order. The rectangle above can be named as ABCD, CBAD, or other sequences, but not ACDB.

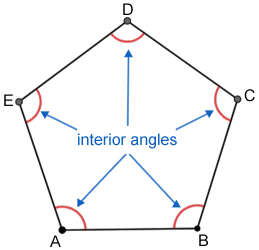
The vertices of a polygon are also the vertices of the interior angles of the polygon. The pentagon ABCDE below shows the interior angles at each of its points.

Vertices of solids

In solid geometry, a vertex is the point where at least 3 edges meet.

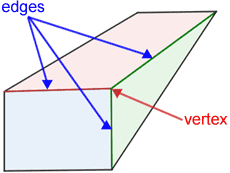
One of the vertices of the five-sided polyhedron (pentahedron) above is shown. Notice that the 3 edges displayed meet at the vertex. The pentahedron has a total of 6 vertices.

A square pyramid has 5 vertices.

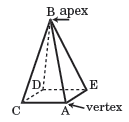
In the pyramid above, A, B, C, D, and E are the vertices. Point B is the highest point in relation to the base of the pyramid. This point is known as the apex of the pyramid.

Circles and vertices

Although circles, as well as other curved shapes, do not have any vertices, there are still angles within circles that do have vertices. For example, the central angle of a circle is the angle whose vertex is always the center of the circle.

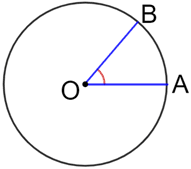
For the circle with center O above, ∠AOB is a central angle since its vertex, O, is also the center of the circle.

Vertices and analytic geometry

In analytic geometry, the vertex of the graph of a parabola is the graph's maximum point or minimum point.

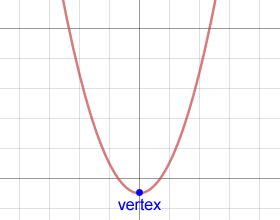
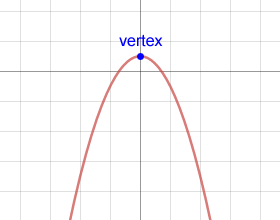
The vertices for the graphs of the other conic sections are critical points that help define their graphs.

There are 2 vertices for the graph of an ellipse.