Ellipse
An ellipse is a 2D figure in the shape of an oval. We usually think of it as looking like a "flattened" or "stretched" circle. The figure below shows two ellipses.
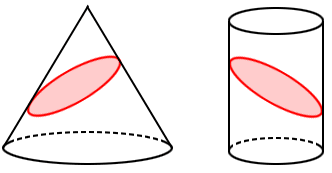
A plane cutting a cone or cylinder at certain angles can create an intersection in the shape of an ellipse, as shown in red in the figures below.
Definition of an ellipse
Mathematically, an ellipse is a 2D closed curve where the sum of the distances between any point on it and two fixed points, called the focus points (foci for plural) is the same.
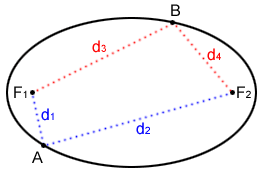
Two points, A and B, are on the ellipse shown above. The focus points for the ellipse are at F1 and F2. The sum of the distances from A to the focus points is d1 + d2 and the sum of the distances from B to the focus points is d3 + d4.
Since A and B are on the ellipse, d1 + d2 = d3 + d4. This is true for any point on the ellipse.
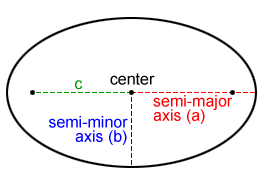
Axes of an ellipse
The midpoint, C, of the line segment joining the foci is the center of the ellipse. The chord through the foci is the major axis of the ellipse, and the chord perpendicular to it through the center is the minor axis. The endpoints of the major axis are called vertices. The major axis and the minor axis perpendicularly bisect each other.
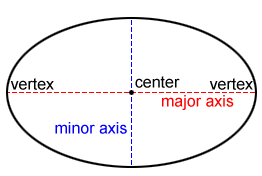
The semi-major and semi-minor axes are one-half the length of the major and minor axes respectively. The distance between the two foci follows this relationship:
c2 = a2 - b2
where a and b are the length of the semi-major and semi-minor axes. The distance between the center and one focus is c (The distance between the two foci is 2c).
Coordinate Geometry and ellipses
In the coordinate plane, an ellipse can be expressed with equations in rectangular form and parametric form.
Rectangular form
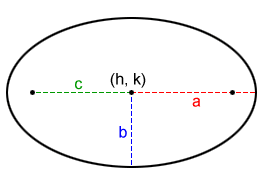
In the coordinate plane, the standard form for the equation of an ellipse with center (h, k), major axis of length 2a, and minor axis of length 2b, where a > b, is as follows.
| Horizontal major-axis | Vertical major axis |
|---|---|
 |
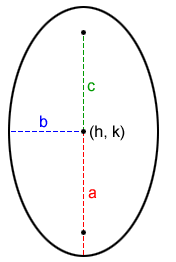 |
Notice that the values for a and b are switched when the major axis is vertical.
If the center is the origin, then the equations simplify to,
| (horizontal major axis) | ||
| (vertical major axis) |
Example:
Write and graph the equation of an ellipse in standard form that has its center at (6, 3), has a horizontal major axis with a length of 10 units, and whose foci have a distance 3 units from the center.
Since we are told the ellipse has a horizontal axis, we use to write its equation in standard form.
The length of the major axis is 10, so .
The foci are 3 units from the center, so c = 3. Using c2 = a2 - b2 to find b:
| 32 = 52 - b2 |
| 9 = 25 - b2 |
| b2 = 16 |
| b = 4 |
A center of (6, 3) means that h = 6 and k = 3 so the equation is,
Parametric form
In parametric form, the equation of an ellipse with center (h, k), major axis of length 2a, and minor axis of length 2b, where a > b and θ is an angle in standard position can be written using one of the following sets of parametric equations.
when the major axis is horizontal
x = h + a·cos(θ), y = k + b·sin(θ)
when the major axis is vertical
x = h + b·cos(θ), y = k + a·sin(θ)
It should be noted that cos(θ) and sin(θ) can be interchanged in either set of parametric equations without affecting their outcomes.
Eccentricity
The eccentricity, e, of an ellipse is the ratio of the distance from the center to a focus (c) to the length of the semi-major axis (a), or . It tells us how "stretched" its graph is. Refer to the figure below for clarification.
The greater the eccentricity, the more "stretched" out the graph of the ellipse will be. The smaller the eccentricity, the more circular the ellipse will look. The following figure shows ellipses with different eccentricities.
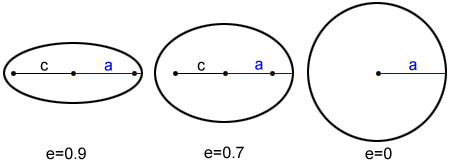
As the foci get closer to the center, c gets closer in length to zero and the eccentricity gets closer to a ratio of zero. A circle has no or zero eccentricity.
Area of an ellipse
The area, A, of an ellipse is π times the product of the lengths of the semi-major (a) and semi-minor axis (b):
A = πab
