Angle bisector

An angle bisector is a line segment, ray, or line that divides an angle into two congruent adjacent angles.

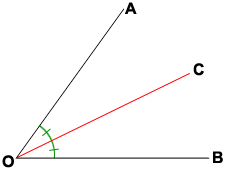
Line segment OC bisects angle AOB above. So, ∠AOC = ∠BOC which means ∠AOC and ∠BOC are congruent angles.

Example:

In the diagram below, TV bisects ∠UTS. Given that ∠STV=60°, we can find ∠UTS.

Since TV bisects ∠UTS, ∠UTV = ∠STV and ∠UTS = ∠UTV + ∠STV, so ∠UTS = 60° + 60° = 120°.

Bisecting an angle with compass and ruler

In geometry, it is possible to bisect an angle using only a compass and ruler. To do so, use the following steps:

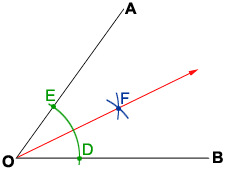
  1. Place the point of the compass on vertex, O, and draw an arc of a circle such that the arc intersects both sides of the angle at points D and E, as shown in the above figure.
  2. Draw two separate arcs of equal radius using both points D and E as centers. Make sure the radius is long enough so the arcs of the two circles can intersect at point F.
  3. Use a ruler to draw a straight ray from O to F. OF bisects the angle AOB.

Things to know about an angle bisector

If a point lies anywhere on an angle bisector, it is equidistant from the 2 sides of the bisected angle; this will be referred to as the equidistance theorem of angle bisectors, or equidistance theorem, for short.

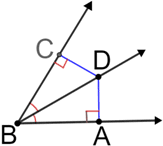
In the figure above, point D lies on bisector BD of angle ABC. The distance from point D to the 2 sides forming angle ABC are equal. So, DC and DA have equal measures.

Conversely, if a point on a line or ray that divides an angle is equidistant from the sides of the angle, the line or ray must be an angle bisector for the angle.

Based on the equidistance theorem, it can be seen that when the two sides that make up an angle are tangent to a circle, the line segment or ray formed by the angle's vertex and the circle's center is the angle's bisector.

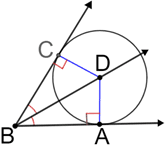
In the diagram above, the two sides of the angle are tangent to the circle and, DC and DA are the distances from the center of the circle to the sides. DC and DA are also the radii of the circle. Since all radii of a circle have equal measure, line BD bisects the angle.

Angle bisector theorem

For a triangle, like the one in the diagram below, if the bisector of angle A intersects side BC at point D, the ratio of the lengths of AB to AC equals the ratio of the length BD to DC. This can be written as: .

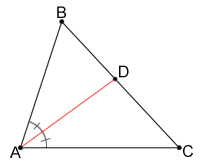
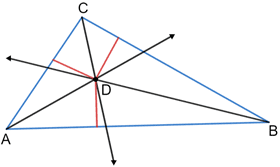
The point at which the three interior angle bisectors intersect is known as the incenter of the triangle. Referencing the diagram below, the three bisecting rays intersect at point D. Point D is the incenter of the triangle and is a point that is equidistant from the three sides of the triangle.