Perpendicular bisector

A line, ray, or line segment (referred to as segment) that is perpendicular to a given segment at its midpoint is called a perpendicular bisector. To bisect means to cut or divide the given segment into two congruent segments.

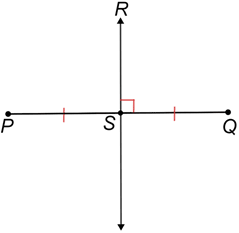
In the diagram above, RS is the perpendicular bisector of PQ, since RS is perpendicular to PQ and PS≅QS.

Additionally, since PS≅QS, point S is the midpoint of PQ. RS has no midpoint since it extends indefinitely in either direction.

Perpendicularly bisecting a line segment using a compass and ruler

In geometry, it is possible to perpendicularly bisect a line segment using only a compass and ruler:

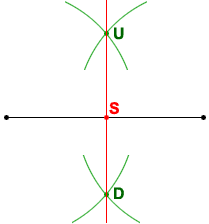
  1. Using each end of the line segment as centers, begin drawing two circles of equal radius such that the arcs of the circles intersect at two points (U and D in the diagram above), one on each side of the segment.
  2. Draw a straight line through U and D. This straight line will intersect with the line segment at point S, the midpoint of the segment.

The line UD is a perpendicular bisector of the line segment. Point S is its midpoint.

Perpendicular Bisector Theorem

The Perpendicular Bisector Theorem states that any point on the perpendicular bisector is equidistant from the segment's endpoints. Let T be on the perpendicular bisector, RS, below.

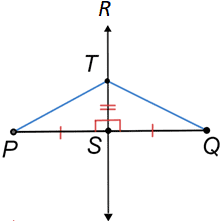
Since RS is perpendicular to PQ, △PST and △QST are both right triangles. Since PS = SQ, △PST≅△QST by the Side-Angle-Side Theorem. So, PS≅SQ, which makes T equidistant from points P and Q. This is true for any point on RS.

The converse of the Perpendicular Bisector Theorem states that if a point in the plane is equidistant from the endpoints of a segment, then it must be on the perpendicular bisector of the segment.

Perpendicular bisectors of triangles

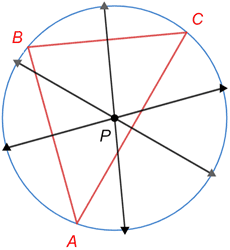
The circumcenter of a triangle is the point at which the perpendicular bisectors of each of the triangle's three sides intersect.


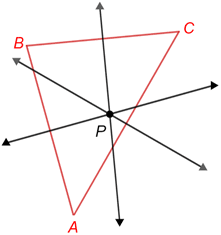
Point P is the circumcenter of triangle ABC above.

The circumcenter of a triangle is also the center of its circumcircle, which is a circle that passes through the three vertices of the triangle, as shown below.