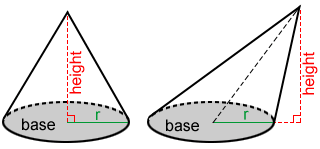
Cone
A cone, usually referred to as a circular cone, is a 3D geometric figure that has a circular base and comes to a point outside the base. Below are two types of cones.
You may think of a traffic cone or an ice cream cone whenever you hear the word cone.

Properties of a cone
A circular cone has a circular base and a curved lateral surface that wraps around the base and meets at a vertex called the apex of the cone. The base and apex lie in different planes.
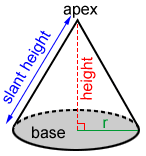
The height of the cone is the distance from the apex to the base. The slant height of a cone is the distance from the apex to a point on the edge of the circular base.
Classifying cones
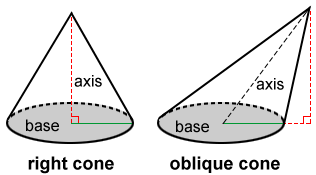
The line segment from the apex to the center of the circular base of the cone, often referred to as the axis of the cone, is used to classify it as a right cone or oblique cone. A right cone's axis is perpendicular to its circular base. The axis for a right cone is also the height of the cone. An oblique cone's axis is not perpendicular to its base.
Cross sections of cones
A cutting plane is a plane that intersects a cone, forming a cross section. Depending on how the cutting plane intersects the cone, a different shape is formed. Any cross section that is parallel to the base of a circular cone forms a circle that is similar (all circles are similar) to the base. This is true for any parallel cross section of a cone.
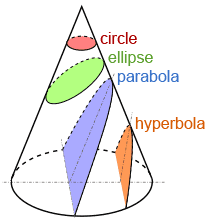
If the cutting plane is not parallel to the base of a circular cone, the cross section forms the shape of an ellipse, a parabola, or a hyperbola, as shown in the figure below. A parabola is formed when the cutting plane is parallel to the opposite slant height line.
Surface area of a right circular cone
The total surface area of a right circular cone is
A = πr2 + πrs
where r is the radius of the base and s is the slant height. In the equation, πr2 is the base area and πrs is the lateral surface area.
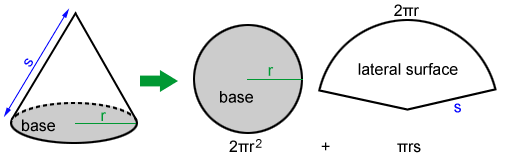
If you cut along the slant height of a right circular cone and lay it out flat, you get a flat lateral surface, or circular sector, as shown above. The arc of this sector is the circumference of the base, which is 2πr. The radius of this sector is s. Therefore, the area of the sector is .
Example:
Find the total surface area of the right circular cone below.
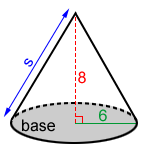
We can use the Pythagorean Theorem to find the slant height, s.
| s2 = 62 + 82 = 100 |
| s = 10 |
Using the formula for the total surface area with r = 6 and s = 10:
| A = π×62 + π×6×10 |
| A = 96π or 301.59 |
Volume of a cone
The formula for the volume, V, of a cone is the same as the volume for a pyramid, which is:
where B is the area of the base and h is the height.
Since the base for a cone is a circle, the base area is B=πr2. Therefore, the volume of a cone is:
where r is the radius of the base.