Prism
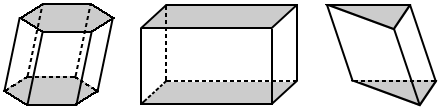
A prism is a space figure with two parallel bases that are polygons of the same size and shape. All other faces of a prism are rectangles, squares, or parallelograms. The following are a few examples:
Properties of a prism
The two parallel and congruent faces of a prism are called bases. The other faces of a prism are called lateral faces. The number of lateral faces in a prism is the same as the number of sides of its polygonal bases. The line segments created by two intersecting faces are called edges. The vertices are points where three or more edges meet.
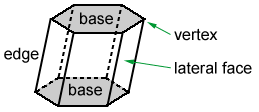
The hexagonal prism above has a total of 8 faces. It has 6 lateral faces that are parallelograms and 2 bases that are hexagons. It also has 18 edges and 12 vertices.
Any cross section that is parallel to the bases of a prism forms a polygon that is congruent to the bases.
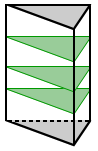
Three triangular cross sections of the triangular prism are shown above. They are congruent to the two triangular bases of the prism since they are formed by cross sections that are in planes parallel to the bases. This is true for any parallel cross section of a prism.
Prism classifications
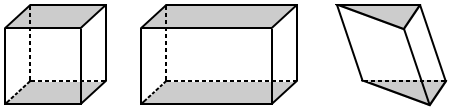
We typically name a prism based on the shape of its polygonal bases. The figure below shows some examples of prisms. From left to right, a square prism, rectangular prism, and triangular prism are shown:
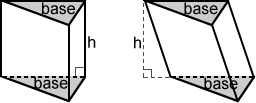
Right prisms and oblique prisms
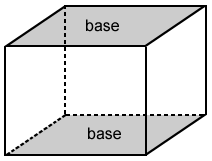
Prisms can also be further classified based on how their lateral faces intersect with their bases. If all the lateral faces are perpendicular to the bases, the prism is called a right prism. If not, it is called an oblique prism.
| Right prism | Oblique prism |
|---|---|
 |
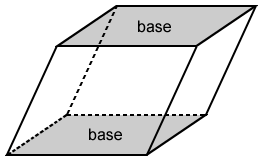 |
| right rectangular prism | oblique rectangular prism |
Regular prisms
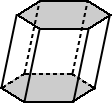
If the base of a prism is a regular polygon, it is called a regular prism. Otherwise, it is an irregular prism. Often, a regular prism is implied to be a right prism.
| Regular prism | Irregular prism |
|---|---|
 |
 |
| regular hexagonal prism | irregular hexagonal prism |
Volume of a prism
The volume of prism is:
V = B·h
B is the area of the base and h is the height of the prism. If it is a right prism, the height is the length of the edge of the side of the prism. If it is an oblique prism, the height is the distance from any point of one base to another.