Chord
A chord is any line segment whose endpoints lie on a circle. The diameter is a special kind of chord that passes through the center of a circle. It is also the longest possible chord for a given circle.
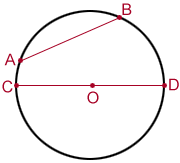
In the diagram above, line segment and are both chords. Line segment is also a diameter of the circle since it passes through the center O.
Intersecting chords
If two chords intersect inside a circle, four angles are formed. Additionally, the endpoints of the chords divide the circle into arcs.
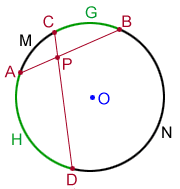
In the diagram above, chords and intersect at P forming 2 pairs of congruent vertical angles, ∠APD≅∠CPB and ∠APC≅∠DPB. The chords also divide the circle into four arcs, .
Intersecting chords theorem
If two chords intersect inside of a circle, the product of the lengths of their respective line segments is equal. In the diagram above, if chords and intersect at point P, the intersecting chords theorem states:
AP · PB = CP · PD
Example:
If AP = 4, CP = 5, and PB = 10, we can find the length of chord CD as follows,
5 · PD = 4 · 10
5 · PD = 40
PD = 8
Since CD = CP + PD,
CD = 5 + 8 = 13
Angles of intersecting chords theorem
The angles formed by intersecting chords inside a circle can be determined using the arcs they intercept. Referencing the same diagram used above:

Inscribed angle theorem
An inscribed angle for a circle is formed when two chords intersect at one of their endpoints on the circle.
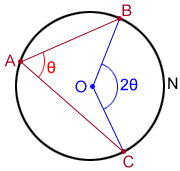
In the diagram above, chords and intersect on a circle at point A forming the inscribed angle, ∠BAC. The measure of the inscribed angle ∠BAC or ∠θ is one-half the measure of its intercepted arc so,
Example:
If ∠BAC=70° we can find the measure of .
Did you know?
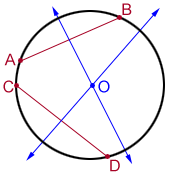
It is easier to find the center of a circle than you think. You can do so with a ruler and a compass. In the diagram below, first draw 2 non-parallel chords and . Then draw the perpendicular bisectors of the chords. The intersection of the two perpendicular bisectors, O, is the center of the circle.