Acute
Angles can be classified according to their measure. An acute angle is an angle that measures greater than 0° but less than 90° (the measure of a right angle).
Angles can also be classified as obtuse, right, and straight, depending on the measure of their angles.
When identifying or measuring an acute angle, be careful about the rotation from one side of the angle to the other that produces the acute angle.
Example:
In the figure below, ∠MON and ∠PON are adjacent angles that are also complementary. Find the measures of ∠MON and ∠PON.
Since ∠PON and ∠MON are complementary, ∠PON + ∠MON = 90°. If we plug in the expressions for the angle measures we get,
| (2x - 3) + (x + 9) = 90 |
| 3x + 6 = 90 |
| x = 28 |
So, ∠MON = 28 + 9 = 37° and ∠PON = 2×28 - 3 = 53°.
Notice that ∠PON and ∠MON must be acute angles since their sum is equal to the measure of a right angle (90°).
Acute triangle
An acute triangle is a triangle in which each of its interior angles has a measure between 0° and 90°. Since triangle ABC below has interior angles all of which are less than 90° and sum to 180°, it is classified as an acute triangle.
Example:
The 3 angles formed with vertices A,B, and C of the tent below have equal measure. Can you classify the angles for triangle ABC?
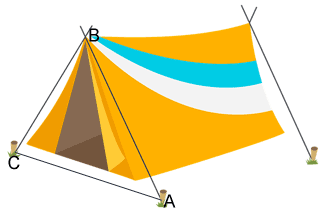
Let x represent the measure of each angle. Then,
| x + x + x = 180° |
| 3x = 180° |
| x = 60° |
So, each angle has a measure of 60° and triangle ABC is an acute triangle. The triangle can further be classified as both an equiangular triangle, since each angle has an equal measure, as well as an equilateral triangle, since each side has an equal measure.
Did you know?
Acute comes from a Latin word meaning sharp (the opposite of obtuse or dull). The vertex of an acute angle is "sharp" when compared with the vertex of an obtuse angle.