Vertical angles
Vertical angles, also referred to as vertically opposite angles, are a pair of non-adjacent angles formed when two lines or line segments intersect. In the vertical angles example below, ∠1 and ∠3 are a pair of vertical angles and ∠2 and ∠4 are a pair of vertical angles.
Real life examples of vertical angles include the letter X, an hourglass, railroad crossing signs, and more.
Vertical angles definition
Vertical angles are the pair of congruent and opposing (non-adjacent) angles formed at the intersection of two lines. Whenever two lines intersect, two pairs of vertical angles are formed. The adjacent angles are supplementary, and the vertical angles may be supplementary but only if the intersecting lines are perpendicular.
The term "vertical" in the case of vertical angles refers to the vertex shared between the four angles formed by two intersecting lines. The vertical angles are not necessarily in an upright position, as we can see in the figure above with angles 2 and 4. Another way to view vertical angles is as a pair of angles where reflecting one across its vertex will line it up with the other angle. Depending on the orientation of the intersecting lines, vertical angles form what looks like the letter "X."
Vertical angles are congruent
The vertical angles theorem states that the vertical angles formed by the intersection of two straight lines are congruent; when two lines intersect, there are two pairs of congruent angles.
Angles 1 and 3 are vertical angles, and therefore congruent. The same is true of angles 2 and 4.
Vertical angle theorem proof
To prove that vertical angles are congruent we use pairs of adjacent angles. In the figure above, since angles 1 and 2 are adjacent and form a straight angle, ∠1 + ∠2 =180°. Also, since angles 2 and 3 are adjacent and form a linear pair, then
| ∠1 + ∠2 = 180° = ∠2 + ∠3 |
| ∠1 = ∠3 |
Thus, ∠1 is congruent to (≅) ∠3 and we can use the same process to show that ∠2 ≅ ∠4.
Vertical angles characteristics
Below are some properties of vertical angles.
- Vertical angles are always congruent.
- Vertical angles share the same vertex but cannot share the same side. If they shared the same side, they would be adjacent angles, and by definition cannot be vertical angles.
- Vertical angles are supplementary (sum to 180°) only if the intersecting lines are perpendicular. In any other case, vertical angles are not supplementary.
- Vertical angles are complementary only if the two angles have measures of 45°. In this case, the other pair of vertical angles must have measures of 135°.
- When two lines intersect, two pairs of vertical angles are formed, and the sum of their angle measures is always equal to 360°.
How to solve vertical angles
There is no formula for calculating vertical angles, but we can find their measures using various angle properties and an understanding of what vertical angles are. Given two intersecting lines, we only need a single angle measure to be able to identify the remaining three.
Example
Find the missing angle measures.
Since the known angle and angle 2 are vertical angles, we know that angle 2 measures 108° as well. Then, since angles 2 and 3 are supplementary angles, we know that their sum is 180°, so to find angle 3, subtract angle 2 from 180°:
Then, since angles 3 and 1 are vertical angles, the measure of angle 1 is also 72°. We can confirm this since we know that the sum of the four angles formed when two lines intersect is 360°, so:
Intersecting chord theorem of angles
When two chords of a circle intersect inside the circle, two pairs of vertical angles are formed. The measure of the angle formed is half the sum of the arcs subtended by the vertical angles formed by the chords of the circle:
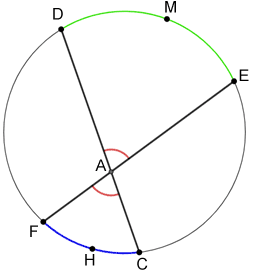
Referencing the diagram above,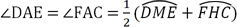 
. This is true for any vertical angles formed by two chords inside the circle. The chords do not have to intersect at the center of the circle for this theorem to be true.