Adjacent
The term "adjacent" is often used to describe angles. It is also used to describe the sides of polygons.
Adjacent angles
Adjacent angles are two angles in a plane that have a common vertex and a common side. They do not have any common interior points. In other words, they do not share any "inside space."
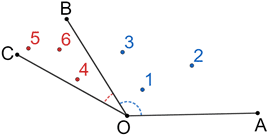
∠COB and ∠AOB are adjacent angles since they have a common vertex, share a common side, and share no common interior points.
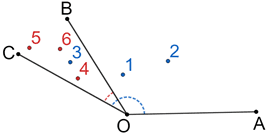
∠COB and ∠AOC are non-adjacent angles. Although they have a common vertex and share a common side, they also share some common interior points, so they cannot be adjacent angles.
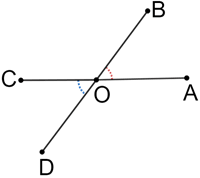
∠COD and ∠AOB are non-adjacent angles. Although they share a common vertex and do not share any common interior points, they do not share a common side, so they cannot be adjacent angles. ∠COD and ∠AOB are referred to vertical angles.
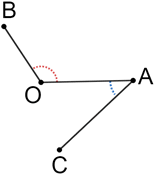
∠CAO and ∠BOA are non-adjacent angles. They share a common side and do not share common interior points, but they do not share a common vertex, so they cannot be adjacent angles.
Example:
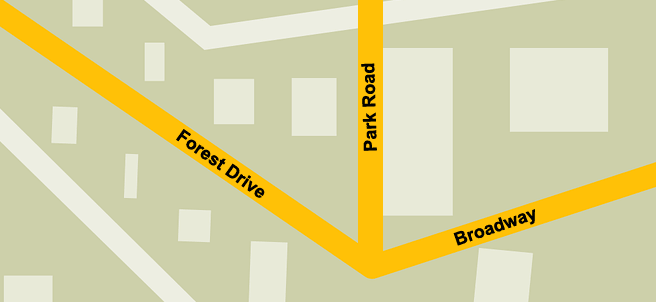
The 3 roads above form two adjacent angles. The two angles formed share a common side of Park Road and the intersection of the 3 roads is the common vertex for the 2 adjacent angles. In this case, it would probably be wise to put a traffic signal at the vertex.
Knowing that 2 angles are adjacent is useful for finding the measure of one of the adjacent angles given the measure of the other.
Example:

In the diagram above ∠POM = 67° and ∠MON=52°. Since ∠PON and ∠MON are adjacent angles the measure of their sum is ∠POM,
| ∠PON + ∠MON = ∠POM |
| ∠PON + 52° = 67° |
| ∠PON = 15° |
Adjacent sides
Adjacent sides are two sides of a polygon or other shapes that have a common vertex.
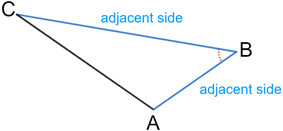
In the triangle above, and are adjacent sides since they share the same vertex, B. and and and are also adjacent sides.
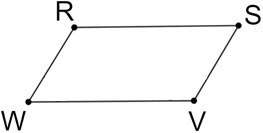
In the parallelogram above, sides and , and are two examples of adjacent sides since they have common vertices. In contrast, sides and and and are not adjacent sides since they do not share a vertex.
