Congruent angles

Congruent angles are angles that have the same measure.

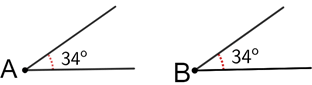
The measure of angles A and B above are both 34° so angles A and B are congruent or ∠A≅∠B, where the symbol ≅ means congruent.

The sides of the angles do not need to have the same length or open in the same direction to be congruent, they only need to have equal measures.

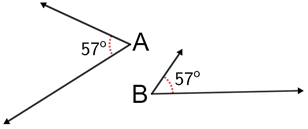
The measure of angles A and B above are 57° so, ∠A=∠B, and ∠A≅∠B,.

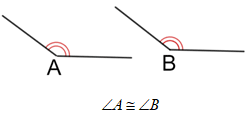
Congruent angles can also be denoted without using specific angle measures by an equal number of arcs placed around the vertices of two angles, as shown below.

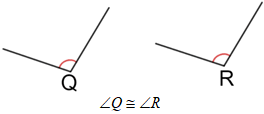
Uses of congruent angles

Whenever an angle is bisected, two congruent angles are formed.

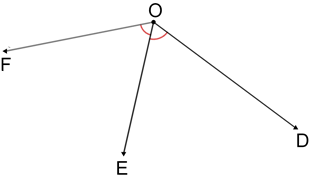
In the figure above, ∠DOF is bisected by OE so, ∠EOF≅∠EOD.

Whenever two lines intersect at a point the vertical angles formed are congruent.

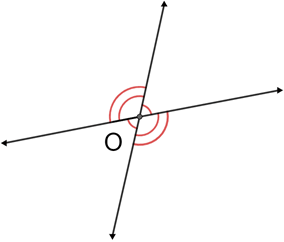
The two lines above intersect at point O so, there are two pairs of vertical angles that are congruent.

Two polygons are said to be similar when their corresponding angles are congruent. The corresponding sides of similar shapes are not necessarily congruent. This means that all congruent shapes are similar, but not all similar shapes are congruent.

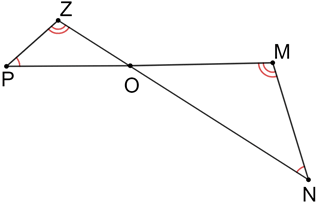
In the figure above, PN and ZN intersect at point O. If ∠P≅∠N and ∠Z≅∠M, then triangle POZ is similar to triangle NOM since the vertical angles at point O forms the 3^rd pair of congruent angles for both triangles.

Two polygons are congruent when their corresponding angles and corresponding sides are congruent.

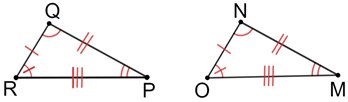
In the figure above, △PQR≅△MNO since ∠P≅∠M, ∠Q≅∠N, and ∠R≅∠O. Additionally, the three sides of △PQR are equal to the three corresponding sides of △MNO. Therefore △PQR and △MNO are congruent.

Whenever a quadrilateral's opposite angles are congruent, the quadrilateral forms a parallelogram.

In quadrilateral ABCD above, ∠A≅∠C, ∠B≅∠D so, the quadrilateral is a parallelogram.