Obtuse
Angles can be classified according to their measure. An obtuse angle is an angle that measures more than a right angle but less than a straight angle. So, an obtuse angle has a measure between 90° and 180°.
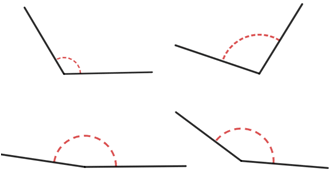
Angles can also be classified as acute, right, and straight, depending on the measure.
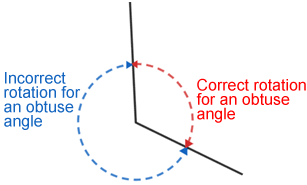
When identifying or measuring an obtuse angle, be careful about the rotation from one side of the angle to the other that produces the angle.
Example:
In the figure below, ∠MON and ∠PON are adjacent angles that are also supplementary. Find the measures of ∠MON and ∠PON and state which angle is an obtuse angle.
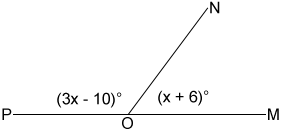
Since ∠MON and ∠PON are supplementary, ∠MON + ∠PON = 180°. If we plug in the expressions for the angle measures, we get,
| (3x - 10) + (x + 6) = 180 |
| 4x - 4 = 180 |
| x = 46 |
So, ∠MON = 46 + 6 = 52°, and ∠PON = 3×46 - 10 = 128°.
∠PON is obtuse since its measure is between 90° and 180°.
Obtuse triangle
The term obtuse is also used in the context of triangles. Whenever a triangle is classified as obtuse, one of its interior angles has a measure between 90° and 180°.
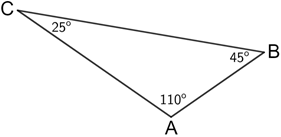
Triangle ABC above is classified as an obtuse triangle since angle A is between 90° and 180°.
It is not possible for a triangle to have more than one obtuse angle. The sum of the measures of the angles in any triangle is 180°, so if one of the angles in the triangle is an obtuse angle, the sum of the other 2 angles must be less than 90° making the other 2 angles acute.
Did you know?
Obtuse comes from a Latin word meaning blunted or dull (the opposite of acute or sharp). The vertex of an obtuse angle is "dull" when compared with the vertex of an acute angle.
See also acute, angles, right, straight.
