Alternate interior angles
When a transversal intersects two lines, it forms two pairs of alternate interior angles. The alternate interior angles are the opposing pair of interior angles formed by the transversal and the two lines.
In the diagram below, transversal l intersects lines m and n. ∠1 and ∠4 are a pair of alternate interior angles and ∠2 and ∠3 are another pair.
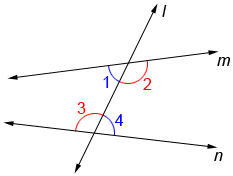
If two lines in a plane are cut by a transversal so that any pair of alternate interior angles is congruent, the lines are parallel. Conversely, if two lines are parallel, any pair of alternate interior angles is congruent.
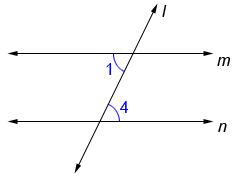
Lines m and n above are cut by transversal l where ∠1≅∠4 so, m//n (// is the symbol for parallel).
Example:
Find the measures of angles 1, 3, and 4 below.
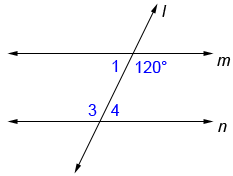
Since lines m and n are parallel, ∠3=120°. Since ∠1 and 120° form a straight angle, ∠1=180°-120°=60°. Similarly, ∠3 and ∠4 form a straight angle so, ∠4=60°.
Alternate interior angles can be used to show similarity for two triangles.
Example:
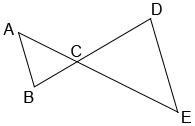
Parallel line segments AB and DE are cut by transversals AE and BD which intersect at point C. Since alternate interior angles are congruent, we can show that △ABC is similar to △EDC.
| ∠A≅∠E, ∠B≅∠D | congruent alternate interior angles |
| ∠ACB≅∠ECD | vertical angles are congruent |
| △ABC~△EDC | AA similarity postulate |
Note: It is not necessary to prove triangles are similar by showing three pairs of congruent angles. Showing two pairs of congruent angles is sufficient.
