Corresponding angles
In geometry, corresponding angles are pairs of angles formed when a transversal intersects two lines. Refer to the figure below. The corresponding angles are the angles that lie on the same side of the transversal in matching corners. In other words, they occupy the same relative position in the figure. In a pair of corresponding angles, one is an exterior angle and one is an interior angle.
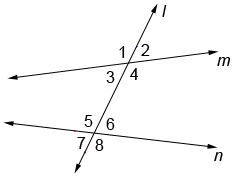
In the figure, transversal l intersects lines m and n. ∠1 and ∠5 are a pair of corresponding angles. Similarly, ∠2 and ∠6, ∠3 and 7, and ∠4 and ∠8 are also corresponding angles.
Corresponding angles can never be adjacent angles. If the angles are adjacent (touch), they are not corresponding angles. This also means that consecutive internal angles, such as angles 7 and 8, can never be corresponding angles.
Corresponding angles are just one type of angle pair. Alternate angles are another type of angle pair. In the figure, angles 6 and 3 are alternate angles; so are angles 5 and 4. Unlike corresponding angles, which lie on the same side of the transversal, alternate angles lie on different sides of the transversal.
Corresponding angles postulate
The corresponding angles postulate states that if two parallel lines are cut by a transversal, the corresponding angles are congruent.
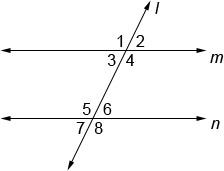
Parallel lines m and n are cut by transversal l above, forming four pairs of congruent, corresponding angles: ∠1 ≅ ∠5, ∠2 ≅ ∠6, ∠3 ≅ 7, and ∠4 ≅ ∠8.
This postulate tells us several things about the eight angles formed when a transversal intersects two lines:
- If one of the angles is a right angle, all of the angles are right angles.
- If one of the angles is acute, 4 of the angles are acute.
- If one of the angles is obtuse, 4 of the angles are obtuse.
- All of the angles can be classified as one of the following types of angles: corresponding, vertical, or adjacent.
The converse of the corresponding angles postulate is also true. If the corresponding angles of two lines cut by a transversal are congruent, then the lines are parallel.
Example:
Using corresponding angles and straight angles, find the measures of the angles formed by the intersection of parallel lines m and n cut by transversal l below.

- ∠2 ≅ ∠60° since they are corresponding angles, and m and n are parallel.
- ∠1 and ∠2 form a straight angle, so∠1=120°.
- ∠5 ≅ ∠120° since ∠1 and ∠5 are corresponding angles, and m and n are parallel.
- ∠7 and ∠5 form a straight angle, so∠7=60°.
- ∠3 ≅ ∠60° since ∠3 and ∠7 are corresponding angles, and m and n are parallel.
- ∠3 and ∠4 form a straight angle, so∠4=120°.
- ∠8 ≅ ∠120° since ∠4 and ∠8 are corresponding angles, and m and n are parallel.
