Linear pair

A linear pair is a pair of adjacent angles whose non-adjacent sides form a line.

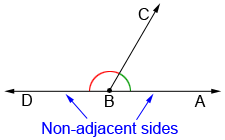
In the diagram above, ∠ABC and ∠DBC form a linear pair. The angles are adjacent, sharing ray BC, and the non-adjacent rays, BA and BD, lie on line AD.

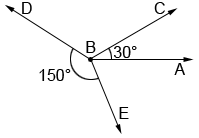
Since the non-adjacent sides of a linear pair form a line, a linear pair of angles is always supplementary. However, just because two angles are supplementary does not mean they form a linear pair. In the diagram below, ∠ABC and ∠DBE are supplementary since 30°+150°=180°, but they do not form a linear pair since they are not adjacent.

Linear pairs in polygons

Linear pairs are often used in the study of the exterior angles of polygons:

In a triangle, an exterior angle is the sum of its two remote interior angles.

Example:

For △ABC above, ∠A+∠C+∠ABC=180°. Also, ∠ABC and ∠DBC form a linear pair so,

∠ABC + ∠DBC = 180°

Substituting the second equation into the first equation we get,

∠ABC + ∠DBC = ∠A + ∠C + ∠ABC

Subtracting we have,

∠DBC = ∠A + ∠C

where ∠DBC is an exterior angle of ∠ABC and, ∠A and ∠C are the remote interior angles.

The sum of the exterior angles of any polygon is 360°. This can be shown by using linear pairs. The sum of the interior angles of an n-side polygon is 180(n-2)°. There are n angles in the polygon, so there are n linear pairs. Thus, the sum of the exterior angles is:

180n° - 180(n-2)° = 360°

For regular polygon, all of the angles of a are equal. Therefore, all the exterior angles are equal, and can be found by dividing 360° by the number of angles .

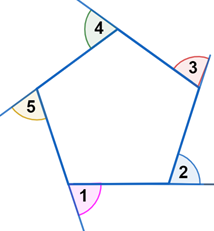
In the regular pentagon above, n = 5. Therefore, the exterior angles measure = = 72° each.