Complementary
Complementary angles are two angles whose measures have a sum of 90°. Each angle is the complement of the other.
Complementary angles can be adjacent or non-adjacent.
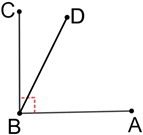
For a right triangle, the two non-right or oblique angles must be complementary.
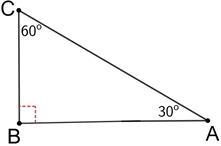
In right triangle ABC above, ∠B = 90° and ∠A + ∠C = 90° so, the nonadjacent angles A and C are complements of each other.
You can determine the complement of a given angle by subtracting it from 90°. For example, the complement of 28° is 62° since 90° - 28° = 62°.
Example:
Look at the diagrams below and see if you can identify the complementary angles.
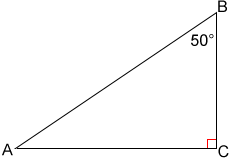
In right triangle ABC above, ∠C = 90° so angles A and B are complementary and, ∠A + 50° = 90°, then ∠A = 40°.
Since two angles do not need to be adjacent to be complementary, given enough information, we do not even need to have a diagram of complementary angles to figure them out.
Example:
Let ∠α and ∠θ be 2 angles that have the variable x in common. If ∠α and ∠θ are complementary where ∠α = (2x - 8)° and ∠θ = (x + 14)°, then
| (2x - 8)° + (x + 14)° = 90° |
| 3x + 6° = 90° |
| x = 28° |
So, ∠α = (2×28 - 8)° = 48° and ∠θ = (28 + 14)° = 42°. Note that 48° + 42° = 90° verifies that ∠α and ∠θ are complementary.
In the study of Trigonometry, the sine value of an angle is equal to the cosine value of its complement. Also, the tangent value of an angle is equal to the cotangent value of its complement. So,
| sin(θ) = cos(90°-θ) and sin(90°-θ) = cos(θ) |
| tan(θ) = cot(90°-θ) and tan(90°-θ) = cot(θ) |
| where the complement for θ is 90°-θ |
Did you know?
Trigonometry is a branch of mathematics that studies the relationships between the side lengths and the angles of triangles. From the Greeks, trigonon means triangle, and metron means to measure.
