Parallel lines
Parallel lines are lines in the same plane that do not intersect. Line segments and rays that are parts of parallel lines are also parallel.
What are parallel lines
Parallel lines are coplanar lines that are equidistant from each other throughout their entire lengths. Parallel lines never intersect. Some real life examples of parallel lines are railroad tracks. For the railroad tracks to work properly and allow a train to move across them, they cannot ever intersect.

Parallel lines symbol
The symbol to show parallel lines is "//". In the figure below, m//n.
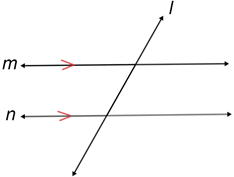
You can also place arrows on the lines, as in the figure above, to show that they are parallel.
Transversals of parallel lines
When 2 lines are cut (intersected) by a third line, called a transversal, 8 angles are formed.
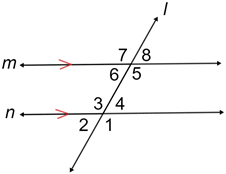
The following terms are used to refer to the angle pairs formed by a transversal and a pair of parallel lines.
- Corresponding angles - angles that occupy the same relative position when a transversal cuts 2 parallel lines. ∠1 & ∠5, ∠2 & ∠6, ∠3 & ∠7, ∠4 & ∠8 are corresponding angles.
- Supplementary angles - either of 2 angles whose sum is 180°. ∠2 & ∠3, ∠6 & ∠7, ∠1 & ∠4, ∠5 & ∠8 are supplementary angles.
- Alternate interior angles - angles formed on the inside of two parallel lines cut by a transversal. ∠3, ∠4, ∠5, ∠6 are alternate interior angles.
- Alternate exterior angles - angles formed on the outside of two parallel lines cut by a transversal. ∠1, ∠2, ∠7, ∠8 are alternate exterior angles.
- Consecutive interior angles - angles formed on the inside of the transversal that are supplementary; also referred to as co-interior angles. ∠3 & ∠6, ∠4 & ∠5 are pairs of consecutive interior angles.
- Vertical angles - pairs of congruent angles formed by the intersection of two straight lines. ∠1 & ∠3, ∠2 & ∠4, ∠5 & ∠7, ∠6 & ∠8 are vertical angles.
Properties of angle pairs
Several relationships exist among these angles. Referencing the above figure:
- Alternate exterior angles are congruent, so ∠1≅∠7 and ∠2≅∠8.
- Alternate interior angles are congruent, so ∠3≅∠5 and ∠4≅∠6.
- Corresponding angles on the same side of the transversal are congruent, so ∠1≅∠5, ∠2≅∠6, ∠3≅∠7, and ∠4≅∠8.
- Consecutive interior angles are supplementary, so ∠3 + ∠6 = 180° and ∠4 + ∠5 = 180°.
- Exterior angles on the same side of the transversal are supplementary, so ∠1 + ∠8 = 180° and ∠2 + ∠7 = 180°
In summary, ∠1, ∠3, ∠5, ∠7 are congruent and ∠2, ∠4, ∠6, ∠8 are also congruent. ∠1, ∠3, ∠5, ∠7 are supplementary to ∠2, ∠4, ∠6, ∠8, respectively.
Also, if any of the eight angles formed by two parallel lines and a transversal is a right angle, all the angles formed are right angles and the transversal is perpendicular to the two parallel lines.
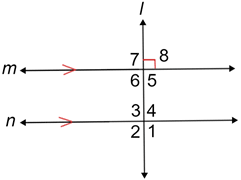
How do you know if two lines are parallel
Below are some of the key properties of parallel lines that can be used to determine if two lines are parallel.
- Parallel lines are always equidistant from each other.
- Parallel lines never intersect at any point along their lengths.
- The slopes of two parallel lines are always equal.
- If two lines are parallel to the same line, they are parallel to each other.
Parallel lines cut by a transversal have the following properties:
- Corresponding angles are congruent.
- Alternate interior angles are congruent.
- Alternate exterior angles are congruent.
- Consecutive interior angles on the same side of the transversal are supplementary.
Slope of parallel lines
In coordinate geometry, parallel lines have the same slope. The converse is also true; if two lines have the same slope, the two lines are parallel unless they overlap.
The blue line below is the graph of the equation y = 2x + 3 and the black line is y = 2x - 4. The slope for both lines is, m = 2. Two vertical lines are still parallel even though their slopes are undefined.
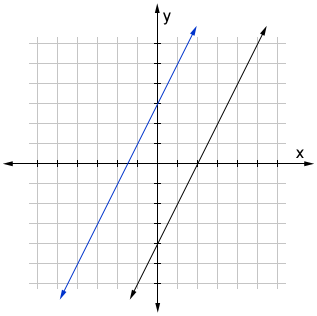
Knowing that two lines are parallel is useful for finding the equation of a line even when given little information about it.
Example:
Suppose a line contains the point (5, -2) and is parallel to the line that has an equation of y = 2x + 6.
The slope of the given line is 2.
Using the point-slope formula, we have,
| y - (-2) = 2(x - 5) |
| y = 2x - 12 |
Parallel lines equations
The equation of a parallel line can be written in various forms, such as slope-intercept form:
y = mx + b
where m is the slope and b is the y-intercept. Recall that the slopes of two parallel lines are always equal. Thus, if we know the slope of one parallel line, it is possible to write the equations for an infinite number of lines parallel to it. For example, given the line y = 2x + 5, we know that any line with a slope of 2, that does not have a y-intercept of 5, will be parallel to the given line. Thus, the general equation for a line parallel to y = 2x + 5 is y = 2x + b for all real values of b except 5.
We can also find the equation of a line that passes through a given point that is parallel to a given line.
Example
Find the equation of a line that passes through the point (1, 2) that is parallel to the line y = 2x + 5.
We know that the line must have a slope of 2 since all parallel lines have the same slope. Now we just have to find the y-intercept of a line with a slope of 2 that passes through the point (1, 2). To do this, we can simply plug the point into the slope-intercept formula, then solve for b:
2 = 2(1) + b
b = 0
Thus, m = 2 and b = 0, meaning that the line passes through the origin and has the equation:
y = 2x
Parallel and perpendicular lines
Parallel and perpendicular lines are often discussed together because they both involve two distinct lines with very specific properties. The table below shows the key differences between perpendicular and parallel lines.
| Parallel lines | Perpendicular lines |
|---|---|

|
|
| Never intersect (0° between) | Intersect at 90 degree angle |
| Denoted with || | Denoted with ⊥ |
One simple way to visualize parallel lines is to think of the letters Z and N. If we remove the diagonal that forms the letters, we are left with either two parallel horizontal lines or two parallel vertical lines. Similarly, we can think of the letters T and L for perpendicular lines. Imagine extending each stroke of the letters. Doing so forms two perpendicular lines.
