Octagon
An octagon is a polygon that has eight sides.
What is an octagon
An octagon is a closed 2D shape that has 8 sides and 8 angles.
Octagon shape
The shape of an octagon depends on the type of octagon. An irregular octagon just needs to have 8 sides and 8 angles but can take on almost any shape. A regular octagon has sides that have the same length and angle measures that are all the same. A stop sign is an example of an everyday object is in the shape of an octagon. The figure below shows some irregular and regular octagons.
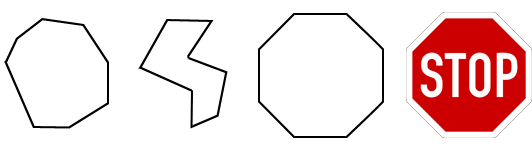
Octagon types
Pentagons are classified as as either regular or irregular and concave or convex.
Regular octagon
A regular octagon is an octagon whose sides are equal in length and whose interior angles are equal in measure.
- Since each of the eight interior angles in a regular octagon are equal in measure, each interior angle measures 1080°/8=135° as shown below.
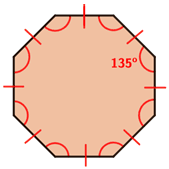
- Each exterior angle for a regular octagon has an equal measure. The exterior angles of a regular octagon have an angle of 45°.
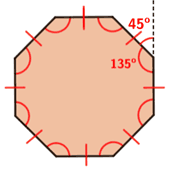
- Sides of a regular octagon are equal in length, and the opposite sides of a regular octagon are parallel.
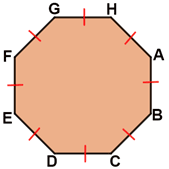AB=BC=CD=DE=EF=FG=GH=AH and //, //, //, //
Irregular octagon
If not all of the sides and interior angles of an octagon are equal, it is an irregular octagon. The octagon below has varying sides and angles, so it is irregular.
Convex octagon
A convex octagon is an octagon in which no line segment between points passes through the octagon. For this to be true, the interior angles of the octagon must all be less than 180°. The figure below shows an irregular convex octagon. Note that a regular octagon is a convex octagon.
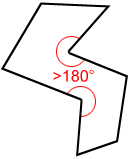
Concave octagon
A concave octagon is an octagon in which it is possible to draw a line segment between two points such that the line segment crosses the inside of the octagon. For this to be true, one or more of the interior angles of the octagon must be greater than 180°.
Octagon properties
Below are some properties of all octagons as well as properties specific to regular octagons.
Properties of all octagons
- 8 angles, 8 sides, and 8 vertices.
- The sum of interior angles is 1080°.
- The sum of all exterior angles is 360°.
- 20 diagonals.
Properties of regular octagons
- All 8 sides are equal.
- All 8 angles are equal.
- Interior angles measure 135° each.
- Exterior angles measure 45° each.
Octagon formula
Below are some formulas for finding the area, perimeter, and diagonal length of a regular octagon.
Area of a regular octagon
The area of a regular octagon with side length s is:
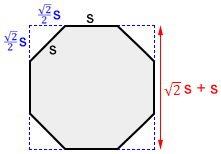
Extending the 4 non-adjacent sides of a regular octagon with side length s will create a square, as shown by the dashed blue lines above. It also forms four 45-45-90 right triangles on the four corners of the square. The hypotenuse of the right triangles are s. The leg lengths of the right triangles are 
. Accordingly, the side length of the square is 
. The area of the octagon can be calculated by subtracting the areas of the four right triangles from the area of the square.
| A = |  |
| = |  |
| = |  |
| = |  |
Example:
What is the area of a regular octagon that has a perimeter of 40?
Since the perimeter is 40, we can find s as follows,
| P = 8 × s |
| 40 = 8 × s |
| s = 5 |
Using :
| A = |  |
| = |  |
| = | 120.71 |
Perimeter of a regular octagon
The perimeter of a regular octagon is:
P = 8a
where a is the length of a side of the regular octagon. If the octagon is irregular, the perimeter is the sum of all the sides.
Diagonal of a regular octagon
The length of the diagonal formed by joining two opposite vertices of a regular octagon is calculated as:
where a is the length of the side of the regular octagon.
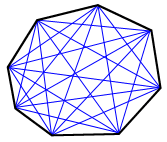
Diagonals of an octagon
A diagonal is a line segment joining two non-consecutive vertices. Five diagonals can be drawn from each vertex. A total of 20 diagonals can be drawn for an octagon. The following figure is an example.
Interior angles of an octagon
The sum of the interior angles of an octagon equals 1080°.
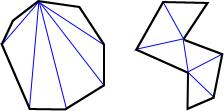
As shown in the figure above, five diagonals can be drawn to divide the octagon into six triangles. The blue lines above show just one way to divide the octagon into triangles; there are others. The sum of interior angles of the six triangles equals the sum of interior angles of the octagon. Since the sum of the interior angles of a triangle is 180°, the sum of the interior angles for the hexagon is 6 × 180° = 1080°.
Symmetry in regular octagons
A regular octagon has 8 lines of symmetry and a rotational symmetry of order 8. This means that it can be rotated in such a way that it will look the same as the original shape 8 times in 360°.
| Lines of symmetry | Rotational symmetry |
|---|---|
 |
 |
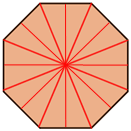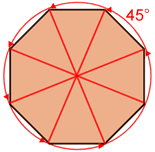| 8 lines of symmetry | Eight 45°angles of rotation |