Bisect
To bisect is to divide a geometric figure into two parts that are the same size and shape.
 |
 |
|
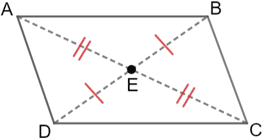
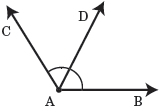
| Point C bisects line segment AB | Ray AD bisects angle BAC | |
 |
 |
|
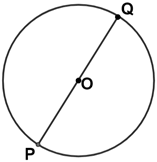
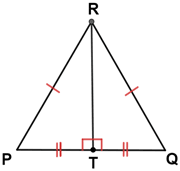
| Diameter PQ bisects circle O | Segment RT bisects triangle PQR | |
Constructing bisectors
In geometry, it is possible to bisect many objects using just a compass and ruler. The following are two examples.
Bisecting a line segment with a compass and ruler
To bisect a line segment using a compass and ruler, use the following steps:
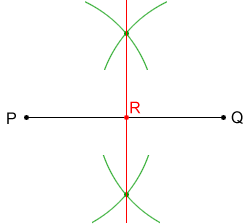
- Place the point of the compass on endpoint P of segment PQ opening it wider than half the segment's length.
- Draw 2 arcs above and below the segment. Repeat this step with endpoint Q. Make sure the arcs have the same radius and draw the arcs long enough so they intersect above and below the segment.
- With a straight edge ruler, draw a line through the points of intersection of the arcs. The line bisects segment PQ at midpoint, R. The line is also perpendicular to segment PQ so it is also the perpendicular bisector of PQ.
Bisecting an angle with a compass and ruler
To bisect an angle using a compass and ruler, use the following steps:
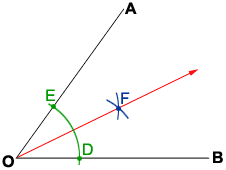
- Place the point of the compass on vertex O and draw an arc such that it intersects both sides of angle AOB at points E and D.
- Placing the compass point at points E and D, draw two separate arcs of equal radius in the interior of angle AOB. Make sure the compass is opened wide enough so the arcs intersect at a point F.
- Use a ruler to draw a ray from O through the point F, which is the intersection of the 2 arcs drawn in step 2. This ray bisects angle AOB.
Bisectors and polygons
The 3 perpendicular bisectors for the sides of any triangle intersect at what is called the circumcenter of the triangle.
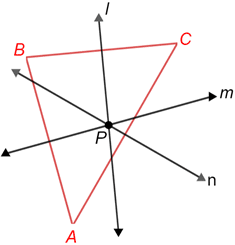
Lines l, m, n are the perpendicular bisectors for the respective sides of triangle ABC. They meet at point P, called the circumcenter of the triangle.
In any parallelogram, the two diagonals bisect each other. Conversely, if the diagonals of a quadrilateral bisect each other, the quadrilateral is a parallelogram.