Skew lines
Skew lines are lines in space that are not in the same plane. They do not intersect and are not parallel.
Imagine a lane on a major highway as one line and the lane or highway passing over it as another line. These two lines are skew lines.

Lines containing edges of a polyhedron is another example of skew lines.
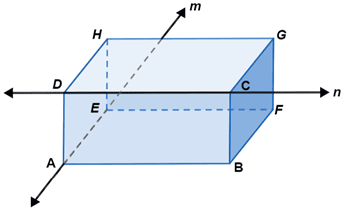
In the figure above, line m contains edge AE and line n contains edge CD. Lines m and n are skew lines since edges AE and CE are not parallel and do not intersect.
Skew lines vs. parallel lines
Skew lines and parallel lines are the two types of lines that never intersect. They are different in that two parallel lines can be on a plane yet two skew lines can never be on the same plane.
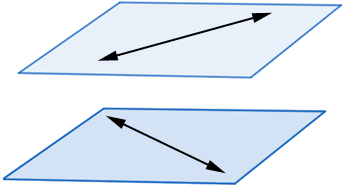
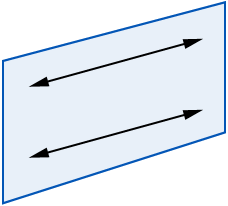
Distance between skew lines
The shortest distance between two skew lines is the length of the line segment that intersects both lines and is perpendicular to both lines. For each pair of skew lines, there is only one line segment that is perpendicular to and intersects both lines.
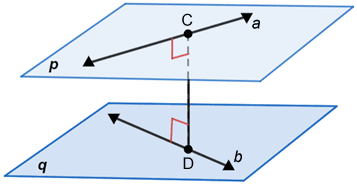
In the figure above, line segment CD is perpendicular to both lines a and b so its length is the shortest distance between the skew lines a and b above.
