Vertical line
A vertical line is a line that goes straight up and down. Examples of vertical lines in real life include fence posts, the legs of a table, the stream of water falling from a tap, and more. Vertical lines are the counterpart to horizontal lines. Examples of each are shown in the figure below.
Vertical line definition
In math, vertical lines are typically found in a coordinate plane, though they can also be found in geometric shapes as lines of symmetry, as well as in other areas of math. In a coordinate plane, a vertical line is defined as a line that is parallel to the y-axis. The y-axis itself is a vertical line, so it follows that any line parallel to it is also a vertical line. Below is the graph of a vertical line that has an x-intercept of (h, 0).
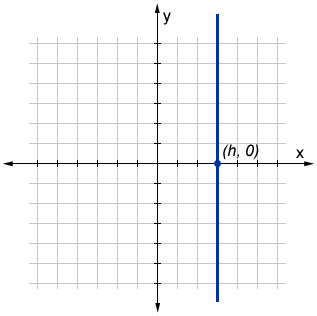
The x-coordinate for any point on the vertical line is h. The y-coordinate can be any real number (we say y is arbitrary) since a vertical line extends infinitely both up and down.
Slope of a vertical line
The slope for a vertical line is undefined. This is because there is no change in x-value, so if we plug values into the slope equation, we will end up with a 0 in the denominator. As an example, using the points (-4, 0) and (-4, 3) for the vertical line below, the slope is,
which is undefined since we can't divide by zero. The graph below shows the vertical line described by these two points.
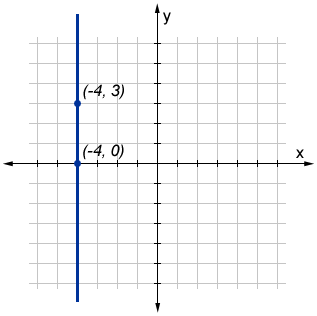
We can see from the figure that there is no change in x, so the slope of the vertical line is undefined or infinite.
Vertical line equation
The equation of a vertical line is,
This is derived from the standard form for the equation of a line, Ax + By = C, where A = 1, B = 0, and C = b:
where b is the x-intercept. In other words, the coordinate of the x-intercept defines the equation of a vertical line.
Properties of a vertical line
Below are some properties of vertical lines:
- Every vertical line intersects the x-axis.
- Every vertical line is parallel to the y-axis.
- Vertical lines have undefined (or infinite) slope.
- Vertical lines have no y-intercept; they are parallel to the y-axis so they do not intersect.
Vertical line test
The vertical line test is used to determine whether a given graph is a function:
- If a vertical line can be drawn such that it intersects a given graph at only one point, the graph is a function.
- If a vertical line cannot be drawn such that it intersects a given graph at only one point, the graph is not a function.
As an example, a circle is not a function, since a vertical line that intersects a circle will always intersect the circle at two points:

In the figure, the blue dotted line represents a vertical line used in the vertical line test. It does not matter where we draw the vertical line; if the line intersects the circle, it does so at two points. Thus, a circle fails the vertical line test and is not a function.
Vertical vs horizontal
Vertical lines and horizontal lines are counterparts. Vertical lines travel up and down while horizontal lines travel left to right. The table below shows some of the differences between horizontal and vertical lines:
| Vertical line | Horizontal line |
|---|---|
| parallel to y-axis | parallel to x-axis |
| undefined slope | 0 slope |
| Equation: x = b | Equation: y = b |
| x-value does not change | y-value does not change |
