Collinear
Points are collinear if they lie on the same line.
What makes points collinear?


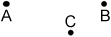
Points that are coplanar lie in the same plane. In the diagram below, points A, B, U, W, X, and Z lie in plane M and points T, U, V, Y, and Z lie in plane N.
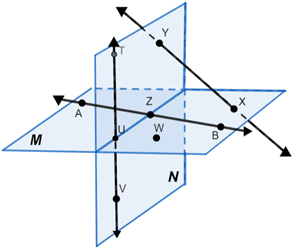
- Points A, Z, and B are collinear. Likewise, points T, U, and V are collinear since they lie on a distinct line.
- Points X and Y are collinear even though they lie in different planes. (It should be noted however, it is possible to construct a plane containing X and Y.)
- Since you can draw a line through any two points there are numerous pairs of points that are collinear in the diagram.
- A set of points that are non-collinear (not collinear) in the same plane are A, B, and X.
- A set of points that are non-collinear and in different planes are T, Y, W, and B.
Features of collinear points
1. A point on a line that lies between two other points on the same line can be interpreted as the origin of two opposite rays.

Point C lies between points A and B on (above). Using these points, we can form two opposite rays, and .
2. Segment lengths. The Segment Addition Postulate states that if A, B, and C are points on the same line where B is between A and C, then AB + BC = AC.

Example:
If AC = 27 and BC = 11 on the diagram above then we can find AB.
| AB + 11 = 27 |
| AB = 16 |
3. Collinear points lie on the same line so the slope between any two points must be equal.
Example:
If (1, 2), (3, 6), and (5, k) are collinear points, what is the value of k?
We can find the value of k by first finding the slope between the two known points. We can then solve for k by equating the slope we just found to an expression for the slope including k as an unknown:
Using points (1, 2) and (3, 6) to find the slope of the line, we get,
The slope between (3, 6) and (5, k) is,
Since the points are collinear the slopes for these two points are equal so,
k = 10
Thus, the value for k is 10 and the coordinate of the 3rd collinear point is (5, 10).
4. There are only 2 vertices that are collinear for any convex polygon in the plane.
For the 6-sided convex polygon below, called a hexagon, you can draw 5 lines from each vertex to the other 5 vertices. However, no combination of any 3 vertices can stay on the same line.