Edge
An edge is a line segment formed by the intersection of two faces of a polyhedron.
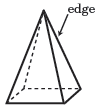 | 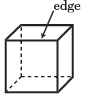 | |
| A square pyramid has 8 edges. | A cube has a total of 12 edges. |
Base edge
A base edge is formed where the base and a lateral face of a space figure meet.
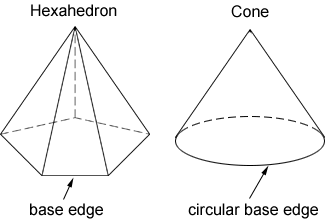
It is important to note that a space figure must be a polyhedron to have edges, so the cone has a base edge, but it is not considered an edge since a cone is not a polyhedron. The base edge pictured for the hexahedron is also an edge since it is the intersection of the hexagonal base and the front triangular lateral face.
Edges and vertices
In solid geometry a vertex is the point where at least 3 edges of a polyhedron meet.
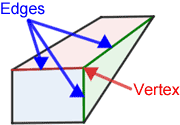
Above, one of the vertices of the pentahedron (five-sided polyhedron) is shown. Notice the 3 edges that are also marked meet at the vertex.
Edges and faces
Three or more edges enclose one of the faces of a polyhedron.
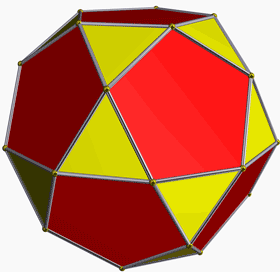
The polyhedron above has triangles and pentagons for its faces. Note the triangle (in yellow) is formed by 3 edges and the pentagon (in red) is formed by 5 edges.
Polyhedra and nets
A two-dimensional model for a polyhedron can be created by cutting some of the edges of its faces.
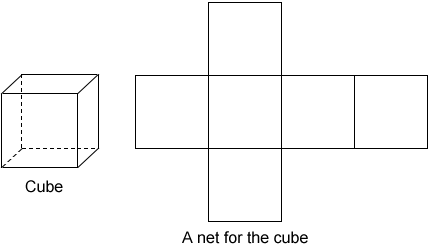
Several of the faces for the cube above are cut along their edges, then laid out such that all the faces are flat (two-dimensional) to create the net for the cube. Note that there are 6 square faces for a cube forming the net.
Euler's Theorem
Euler's Theorem is a formula that determines the number of edges, vertices, or faces for a polyhedron given any two of them for the polyhedron. It states,
| F + V – E = 2 |
| where, |
|
F is the number of faces V is the number of vertices E is the number of edges |
Euler's formula is useful when the polyhedron or the net for the polyhedron is difficult to draw due to the large number of faces it may have.
Example:
Find the number of edges for a dodecahedron that has 20 vertices and 12 faces.
Let V = 20 and F = 12. Then,
| 12 + 20 – E = 2 |
| E = 30 |
So, there are 30 edges.
