Secant

A secant is a line that intersects a curve at a minimum of two different points.

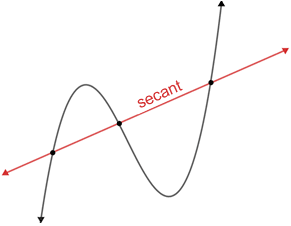
The secant line above cuts (intersects) the curve at three distinct points.

Secants and circles

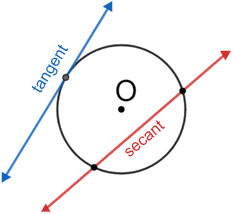
In Geometry, secant lines are often used in the context of circles. The secant line below, in red, intersects the circle with center O, twice. If a line intersects a circle at only one point, it is called a tangent line. The blue line is a tangent line for the circle.

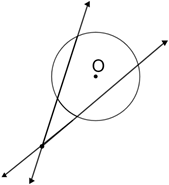
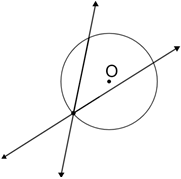
Two nonparallel secant lines for a circle can intersect in one of three ways:

Outside the circle
On the circle
Inside the circle

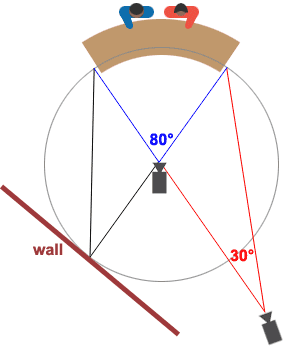
Knowing secant lines and angles formed by their intersects is beneficial when placing T.V. cameras in positions that best capture a television news cast.

Intersecting Secants Theorem

Some interesting properties exist when two secant lines intersect outside of a circle.

For two secant lines that intersect outside of a circle, the product of the measures of one secant line segment and its external segment is equal to the product of the other secant line segment and its external segment:

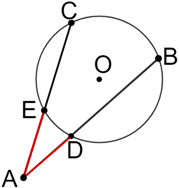
In the figure above, AB and AC are secants for circle O that intersect at A. AD and AE are external segments. The Intersecting Secants Theorem states AB·AD = AC·AE.

Additionally, there is a relationship between the angle created by the secant line segments and the two arcs, shown in red and blue below, that subtend the angle.

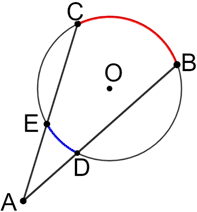
Secants AB and AC form ∠BAC which intersects circle O, creating arcs BC (in red) and DE (in blue). The relationship between the angle and the arcs is 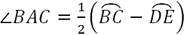.