Perpendicular lines
Perpendicular lines are two distinct lines that intersect at a right angle (90°).
What are perpendicular lines
When two distinct lines form a 90° at their point of intersection, they are perpendicular lines. Lines l and m in the figure below are perpendicular.
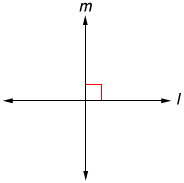
The term "perpendicular" is used to describe more than just lines; it includes line segments, rays, the corners of shapes, and more. As long as some form of two lines meet at a point and create a 90° angle, they are perpendicular. When two lines are perpendicular, it is indicated by 2 line segments that form a box, like those shown in red in the figure. Whenever you see this symbol on some figure, it indicates a 90° angle.
Perpendicular symbol
There are a few different symbols used to indicate that two lines are perpendicular.
- In a graph or on some shape, two line segments that form a square are used. Reference the figure above.
- In writing, the symbol "⊥" is used to indicate perpendicularity. For example, given that m and l are perpendicular, we write l ⊥ m.
Perpendicular and parallel lines
Perpendicular and parallel lines are often discussed together because they both involve two distinct lines with very specific properties. The table below shows the key differences between perpendicular and parallel lines.
| Perpendicular lines | Parallel lines |
|---|---|

|
|
| Intersect at 90 degree angle | Never intersect (0° between) |
| Denoted with ⊥ | Denoted with || |
One simple way to visualize perpendicular lines is to think of the letters T and L. Imagine extending each stroke of the letters; doing so forms two perpendicular lines. Similarly, for parallel lines, we can think of the letters Z and N. If we remove the diagonal that forms the letters, we are left with either two parallel horizontal lines or two parallel vertical lines.
Properties of perpendicular lines
If two lines are perpendicular, 4 right angles are created. In the diagram below, angles 1, 2, 3, 4 are all right angles.
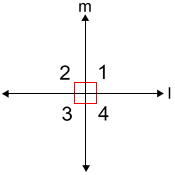
• There can be only one line that is perpendicular to a given line at a given point.
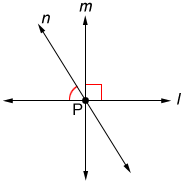
Let lines m, n, and l intersect at point P above. If the angle formed by l and m is a right angle, then the angle formed by lines l and n cannot also be a right angle.
• Two lines are perpendicular if their slopes are negative (or opposite) reciprocals of each other.
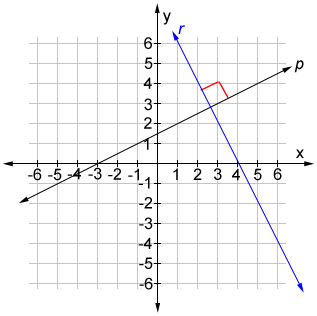
The slope of line p is ½ and the slope of line r is -2, the negative reciprocal of ½, so p and q are perpendicular and meet at a right angle.
Knowing that two perpendicular lines meet at a right angle, or that if their intersection forms a right angle that they are perpendicular, is useful information in working with postulates, theorems, and other properties in Geometry. Below are a few examples.
• If the two non-adjacent sides of two acute adjacent angles are perpendicular, then the angles must be complementary.
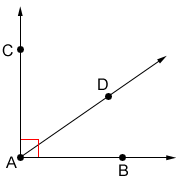
∠BAD and ∠CAD are adjacent angles, with non-adjacent, perpendicular sides and . Since and are perpendicular, ∠BAC is a right angle measuring 90° so, ∠BAD + ∠CAD = 90°.
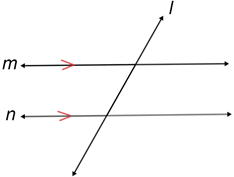
• If a transversal is perpendicular to one of a pair of parallel lines (or several parallel lines), it must be perpendicular to all the parallel lines.
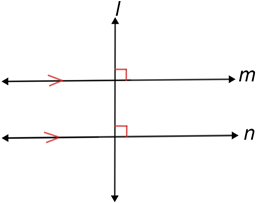
In the diagram above, m//n and l⊥m. Since l⊥m, all four angles formed by the intersection of l and m are right angles. Also, since m//n all four angles are also right angles formed by lines l and n, by the property of corresponding angles of parallel lines being congruent. Thus, line l is also perpendicular to line n.
Did you know?
The x- and y-axis are two lines in the Cartesian coordinate plane that are perpendicular to each other.
Also, each horizontal grid line is perpendicular to each vertical grid line that comprises the grid for the system. The Cartesian coordinate system is also known as an orthogonal (meaning at right angles) coordinate system.
