Intersecting lines
Two or more lines intersect when they share a common point.
If two lines share more than one common point, they must be the same line. If two lines in the same plane share no common point, they must be parallel.
| Same line | Parallel lines |
|---|---|
 |  |
| Line m and n share points A and B so they are the same line. | In the same plane, lines m and n share no common points, so they are parallel. |
Coordinate geometry and intersecting lines
In coordinate geometry, the graphs of lines can be written as equations. Points of intersection can be found using the equations of the lines.
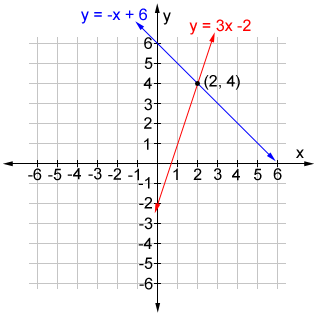
Example:
Find the point of intersection for the lines whose equations are,
y = 3x - 2
y = -x + 6
One method to find the point of intersection is to substitute the value for y of the 2nd equation into the 1st equation and solve for the x-coordinate.
-x + 6 = 3x - 2
-4x = -8
x = 2
Next plug the x-value into either equation to find the y-coordinate for the point of intersection.
y = 3×2 - 2 = 6 - 2 = 4
So, the lines intersect at (2, 4).
Intersecting lines and angles
Angles are formed when two or more lines intersect.
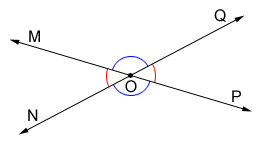
In the figure above, and intersect at point O forming four angles that have their vertices at O.
- Vertical angles are congruent so, ∠MOQ≅∠NOP and ∠MON≅∠QOP.
- Angles ∠MOQ and ∠QOP, and angles ∠NOP and ∠QOP form a linear pair, so ∠MOQ + ∠QOP = 180° and ∠NOP + ∠QOP = 180°.
Forming a plane
The intersection of two lines forms a plane.
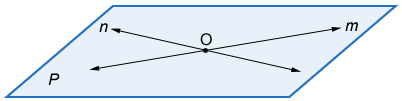
In the figure above, line m and n intersect at point O. Together, lines m and n form plane p.
