Diagonal
For a polygon, a diagonal is a line segment joining two non-consecutive vertices (not next to each other). One of the diagonals is shown for polygons A and B below. All the diagonals are shown for polygons C and D.
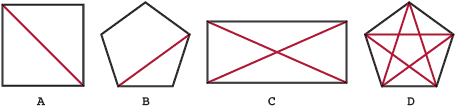
A diagonal for a polygon gives support for physical structures.

Number of diagonals in polygons
The equation can be used to find the number of diagonals, d, for a polygon with n sides called an n-gon. The only polygon that has no diagonals is a triangle since all of its vertices are consecutive.
The following table lists the number of diagonals in common polygons.
| Polygon | # of sides | # of diagonals |
|---|---|---|
| Quadrilateral | 4 | 2 |
| Pentagon | 5 | 5 |
| Hexagon | 6 | 9 |
| Heptagon | 7 | 14 |
| Octagon | 8 | 20 |
| Nonagon | 9 | 27 |
| Decagon | 10 | 35 |
Some properties of diagonals
- A parallelogram is a quadrilateral whose diagonals bisect each other.
- A rhombus is a parallelogram whose diagonals are perpendicular.
- A rectangle is a parallelogram whose diagonals have equal measure (congruent with each other).
- A square is a rhombus whose diagonals have equal measure (congruent with each other).
- The area of a rhombus can be found using the expression
, where d1 and d2 are the diagonals of the rhombus.
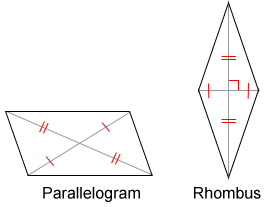
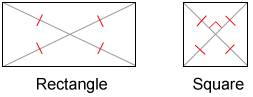
Diagonals and polyhedrons
For a polyhedron, a diagonal is a line segment joining two vertices that are in different faces. The end points of the diagonal share no common edges or faces. These diagonals are sometimes referred to as space diagonals.
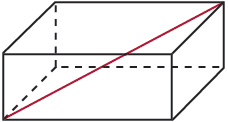
The only polyhedron that contains no space diagonals is the tetrahedron.
The 3 lateral faces that attach to the edges of the base meet at a point called the vertex so, no diagonals can be constructed that are in different faces.
See also polygon, polyhedron.
