Tetrahedron
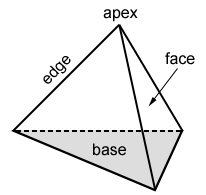
A tetrahedron is a space figure with four triangular faces. The prefix "tetra" means four. Below is a tetrahedron example.

What is a tetrahedron
A tetrahedron is a three-dimensional (3D) figure made up of 4 triangular faces. It is also known as a triangular pyramid. If all of the triangles that form the tetrahedron are congruent equilateral triangles, the tetrahedron is referred to as a regular tetrahedron. The tetrahedron is one of 5 Platonic solids (a Platonic solid is a polyhedron in which all faces are congruent regular polygons and the same number of faces meet at each vertex).
Regular tetrahedron
A regular tetrahedron is the type of tetrahedron referred to as a Platonic solid. Often, when a tetrahedron is referred to as "the" tetrahedron, the tetrahedron being referenced is the Platonic solid. A regular tetrahedron has the following properties:
- Faces: 4
- Edges: 6
- Vertices: 4. Also, all 4 vertices are the same distance from each other.
- Axes of symmetry: 7.
- All four faces are equilateral triangles.
- All faces are the same size and shape.
- All edges are the same length.
- The same number of faces meet at each vertex.
- The tetrahedron is the only Platonic solid with no parallel faces.
- The tetrahedron is the smallest Platonic solid.
Tetrahedron net
A net in geometry is a 2D pattern of polygons that can be modified to form the polyhedron, which in this case is a tetrahedron. A regular tetrahedron net is shown below:

Each of the outer triangles folds inwards to form the tetrahedron. Note that this is not the only possible tetrahedron net.
Properties of a tetrahedron
A tetrahedron is a pyramid with one triangular base and three triangular sides, called lateral faces. The lateral faces share a common vertex called the apex. We usually think of the apex as the "top" of the tetrahedron. An edge is a line segment formed by the intersection of two adjacent faces. A tetrahedron has 4 faces, 6 edges, and 4 vertices. It is the polyhedron that can be formed with the fewest number of faces.
Any cross section that is parallel to the base of a tetrahedron forms a triangle that is similar to its base.
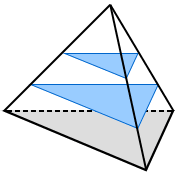
The two triangles, shaded in blue, formed by cross sections parallel to the base of the tetrahedron above, are similar (same shape but not the same size) to the tetrahedron's triangular base.
Right and oblique tetrahedrons
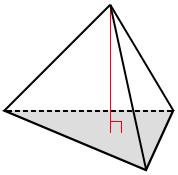
A right tetrahedron is one in which the apex is directly above the center of the base. If the apex is not directly above the center of the base, it is an oblique tetrahedron. The line segment from the apex to the center of the base of a right tetrahedron is perpendicular to the base, and is the height of the tetrahedron.
| Right tetrahedron | Oblique tetrahedron |
|---|---|
 |
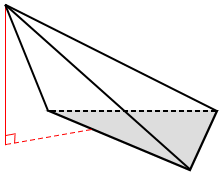 |
| The apex is directly above the center of the base. | The apex is not directly above the center of the base. |
Regular tetrahedron
A regular tetrahedron is a tetrahedron in which all four faces are equilateral triangles. All edges of a regular tetrahedron are equal in length and all faces of a tetrahedron are congruent to each other. A regular tetrahedron is also a right tetrahedron.
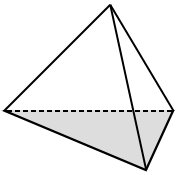
Since all of the faces are congruent equilateral triangles, the tetrahedron above is a regular tetrahedron. Regular tetrahedrons are one of five Platonic solids (a Platonic solid is a polyhedron in which all faces are congruent regular polygons and the same number of faces meet at each vertex).
Irregular tetrahedron
An irregular tetrahedron is a tetrahedron in which the triangles that make up the tetrahedron are not all congruent and equilateral. An oblique tetrahedron is an irregular tetrahedron. the figure below shows an irregular tetrahedron example:
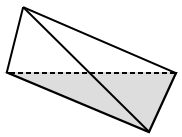
Since the triangles are not all equilateral and congruent, the above figure is an irregular tetrahedron.
Tetrahedron height
Any face opposite a vertex can be considered a base of the tetrahedron. Any height or altitude drawn from the vertex to the opposite face of a regular tetrahedron is equal in length and any height of a regular tetrahedron goes through its center, as depicted in the figure below.
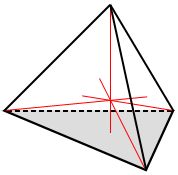
The formula for the height of a tetrahedron is,
where e is the length of the edge.
Tetrahedron surface area
The surface area of a regular tetrahedron is found by first determining the area of one of the faces, then multiplying the area by four. An equilateral triangle with side length e (also the length of the edges of a regular tetrahedron) has an area, A, of
The total surface area, S, of a regular tetrahedron in terms of its edges, e, is
Volume of a tetrahedron
The volume, V, of tetrahedron is
where B is the area of the base and h is the height of the tetrahedron.
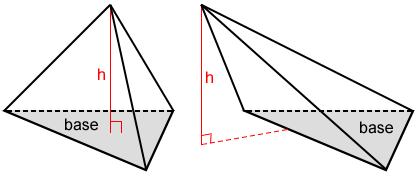
If the tetrahedron is a regular tetrahedron, its volume is
where e is the edge length of the regular tetrahedron.
Example:
If the total surface area of a regular tetrahedron is , what is its volume?
We can find e by substituting the given value in for the total surface area to get
25 = e2
e = 5
Substituting the length of the edge into the volume formula:
