Base
The term "base" can be used in several different mathematical contexts. This page will cover the term as it is used in the context of Geometry and Algebra.
Bases in geometry
The base of a figure is usually thought of as a side or face on which the figure "sits." It can also be thought of as the "bottom" of the figure. However, bases are not limited to being the bottom sides or faces of a figure. Bases are often paired with a height that is perpendicular to the base. This is true for both 2D figures and 3D figures.
Base of a 2D figure
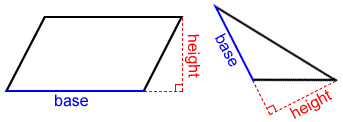
In the figures below, the blue lines indicate the bases of the 2D or plane figures.

Sides can also be considered as bases relative to a height perpendicular to the respective side.
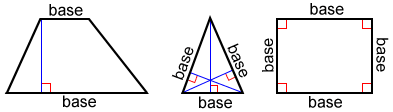
Sometimes, the base needs to be extended to draw its associated height.
Base of a 3D figure
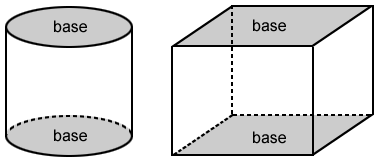
In the figures below, the grey faces indicate the bases of the 3D or space figures.
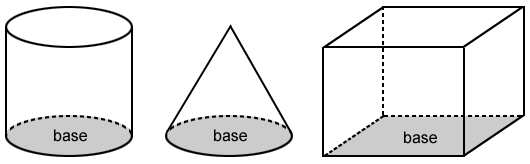
Like 2D figures, broadly speaking, other faces may also be considered as bases.
Base in algebra
A base can also be used as a term when dealing with exponents, logarithms, and solving equations.Bases and exponents
The bases of the expressions 43, x5, and (3x + 1)2 are 4, x, and (3x + 1) respectively.
The number of factors of an exponential expression is determined by the exponent, and the factor is the base. Expanding the expressions above:
| 43 = 4·4·4 = 64 |
| x5 = x·x·x·x·x |
| (3x + 1)2 = 9x2 + 6x + 1 |
Bases and logarithms
For a logarithmic function of the form y = logbx, b is called the base of the logarithm. The function can be written in exponential form as x = by.
Example:
Simplify log381.
| 81 = 3x |
| 34 = 3x |
| x = 4 |
Therefore, log381 is 4.
