Center
The center of something is generally its middle. In the context of geometry, the center is the point in the middle of an object.
Center of a circle
The center of a circle is a point inside a circle that is equal in distance from all of the points on the circle.
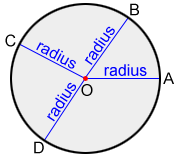
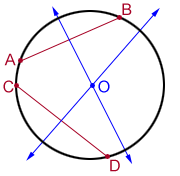
Points A, B, C, and D are equidistant from point O in the circle above, as is any point that lies on the circle. A radius is a line segment that has one endpoint on the center of the circle and the other endpoint on the circle's circumference. A circle has infinitely many radii (plural for radius), and each radius has an equal measure.
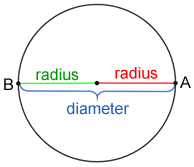
The diameter of a circle is a chord that passes through the circle's center.
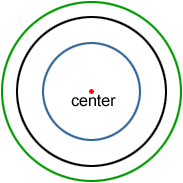
Concentric circles are a set of circles that have the same center.
Constructing the center of a circle
You can construct the center of a given circle with a compass and straightedge. Follow these steps:
- Draw 2 non-parallel chords AB and CD.
- Draw the perpendicular bisectors of the chords. The intersection of the two perpendicular bisectors, O, is the center of the circle.
Center of a circle in coordinate geometry
In coordinate geometry, a circle can be expressed as (x-h)2 + (y-k)2 = r2. The center of the circle with radius r in this equation is located at point (h, k).
Example:
Find the center of the circle given in general form.
x2 + 4x + y2 - 2y - 11 = 0
The equation above can be rearranged as:
(x2 + 4x + 4) + (y2 - 2y + 1) = 16
(x+2)2 + (y-1)2 = 42
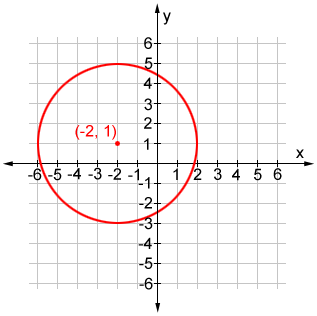
So, the circle has a radius of 4 units and its center is at (-2, 1). The graph of the circle is shown below.
Center of a polygon
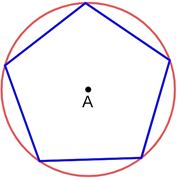
The center of a regular polygon is the same as the center of its circumscribed circle. The center is equidistant from all its vertices.
Center of a sphere
The center of a sphere is a point inside a sphere that is equidistant from all points that form the sphere.

In coordinate geometry, a sphere can be expressed as (x-a)2 + (y-b)2 + (z-c)2 = r2. Using this equation, the center of the sphere with radius r is located at point (a, b, c).
