Dodecahedron

A dodecahedron is a polyhedron with 12 faces. In the figure below are 2 different types of dodecahedrons. The prefix "dodeca" means twelve.

Because of their complex nature, a dodecahedron is a shape that is not commonly seen in everyday life.

Properties of a regular dodecahedron

A regular dodecahedron is a dodecahedron whose faces are all congruent, regular polygons. Otherwise, it is irregular. Regular dodecahedrons are studied more often.

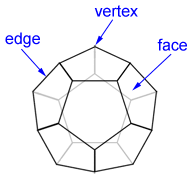
A regular dodecahedron, such as the one shown above, has 12 congruent faces that are regular pentagons, 30 congruent edges, and 20 vertices; an edge is a line segment formed by the intersection of two adjacent faces; a vertex for a regular dodecahedron is a point where 3 edges meet. Regular dodecahedrons are one of five Platonic solids, which are a type of regular polyhedron.

Surface area of a regular dodecahedron

We can find the area of one of the faces and multiply it by twelve to find the total surface area of a regular dodecahedron.

A regular pentagon with side length, e (also the length of the edges of a regular dodecahedron), has an area, A, of

The total surface area, S, of a regular dodecahedron in terms of its edges, e, is,

Volume of a regular dodecahedron

The volume, V, of regular dodecahedron is

where e is the length of the edge of the regular dodecahedron.