Dimensions
In mathematics, dimension has two meanings. Dimension is used as a description of the size of an object. For example, the length and width describe the dimension or size of a rectangle. The length, width, and height describe the dimensions, or size, of a rectangular prism.
Below are two figures along with their stated dimensions.
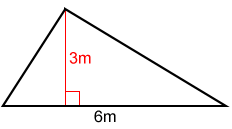 |
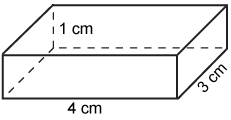 |
|
| The base and height of the triangle above are 6 m and 3 m respectively. | The length, width, and height of the above rectangular prism are 4 cm, 3 cm, and 1 cm respectively. |
The dimension of an object is also defined as the minimum number of coordinates needed to specify any point within a mathematical space, or the number of degrees of freedom of a point that moves on the object. A line, for example, has one dimension because a point can only move along the line. We live in what we know to be a 3D world; therefore, most studies in mathematics are limited to 0D, 1D, 2D, and 3D space, as described below.
Zero-dimensional space
A point describes a position in space but has no size or shape, so it has no, or zero dimensions.
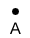
Although a point technically has no size or shape, we use a dot, as shown above, to represent a point.
One-dimensional space
A line or any of its parts (line segment or ray) is one dimensional (1D). In one-dimensional space, any point can be described with one number, as shown in the figure below. Any point on the line can only move along the line. An object in a one-dimensional space, such as a line segment, can be described using just one dimension, length.
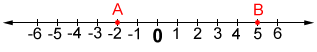
The number line above is 1D. A point can only move left or right along the line. The position of point A can be described with just one coordinate number, -2. The size of AB can be described by its length, 7.
Two-dimensional space
A 2D object has length and width, but no depth. A plane has two-dimensions, length and width and forms a flat surface (such as a piece of notebook paper) extending in both directions infinitely, as shown below.
In a two-dimensional space, any point can be described with two numbers. Any point on a two-dimensional space has two degrees of freedom; a point can move from one position to any position in the space through a combination of moving horizontally and vertically.
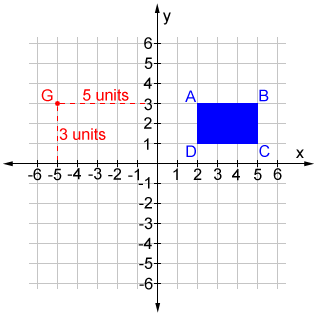
Point G above is graphed in the 2D coordinate plane by moving 5 units left of the origin along the x-axis and 3 units up along the y-axis. The position of G can be described with two numbers (-5, 3). The size of an object, such as the blue rectangle ABCD above, can be described using width and length.
Three-dimensional space
A 3D object has length, width, and depth. The rectangular prism shown below has length, width, and height. Each dimension is measured as a length that is perpendicular to any other dimension. In this case, the width is the depth of the prism.
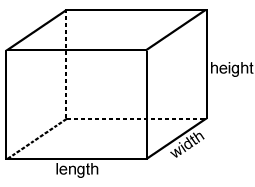
In a three-dimensional space, any point can be described with three numbers. Any point on a three-dimensional space has three degrees of freedom.
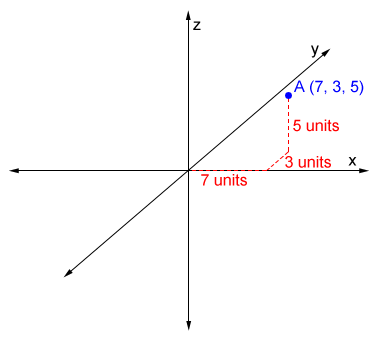
Point A is graphed in the 3D coordinate plane by moving 7 units in the positive direction along the x-axis, 3 units in the positive direction along the y-axis, and 5 units up along the z-axis. The position of A can be described with three numbers (7, 3, 5).
Did you know?
We live in what we know to be a three-dimensional world, having length, width, and height. Mathematicians and scientists have been working to show that many more dimensions in our universe exist.
While we can only visualize the dimensions in a three-dimensional world, the mathematics of string theory and super-string theory have theorized 10 or more dimensions.
