Nonagon
A nonagon is a polygon that has nine sides. It is also referred to as an enneagon or 9-gon. There are various types of nonagons; the figure below depicts a few.
Regular nonagon
A regular nonagon has angles and interior angles that are all equal.
Properties of a regular nonagon
Below are some properties of a regular nonagon, as well as some properties that apply to all nonagons.
- Each interior angle in a regular nonagon measures 140°.
- The sum of all interior angles of a nonagon equals 1260°. This is true of all nonagons, not just regular nonagons, but an irregular nonagon has interior angles with different measures.
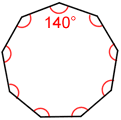
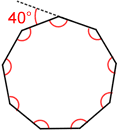
- Each exterior angle of a regular nonagon measures 40°; the sum of all exterior angles is 360°.
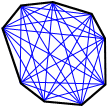
- All nonagons have 27 diagonals.
- The perimeter of a regular nonagon with side a is:
- The area of a regular nonagon with side a is:
Irregular nonagon
An irregular nonagon is a nonagon in which not all sides and angles are equal. Irregular nonagons still share some of the properties of regular nonagons, such as the sum of all its interior angles equalling 1260°. Irregular nonagons can come in many different forms. Below is an example of an irregular nonagon:
Convex and concave nonagons
Irregular nonagons can be categorized as either convex or concave (a regular nonagon can only be convex).
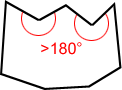
- A convex nonagon is one in which all of the interor angles are <180°. A regular nonagon is convex. The figure below shows an irregular nonagon that is convex.

- A concave nonagon is a nonagon in which one or more interior angles have measures >180°.
Diagonals of convex nonagon
A diagonal is a line segment joining two non-consecutive vertices. A total of twenty-seven distinct diagonals can be drawn for a nonagon. The following figure is an example.

There are 6 diagonals extending from each of the 9 vertices of the nonagon above creating a total of 27 diagonals. The diagonals of a nonagon are drawn by drawing a line segment between the non-adjacent vertices of the nonagon. Note that the number of diagonals in a given polygon can be found using the following formula:
where n is the number of sides in the polygon. Thus, plugging 9 into the formula yields:
Internal angles of a nonagon
The sum of the interior angles of a nonagon equals 1260°.
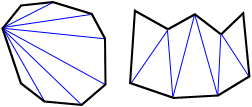
As shown in the figure above, six diagonals can be drawn to divide the nonagon into seven triangles. The blue lines above show just one way to divide the nonagon into triangles; there are others. The sum of interior angles of the seven triangles equals the sum of interior angles of the nonagon. Since the sum of the interior angles of a triangle is 180°, the sum of the interior angles of the nonagon is 9 × 180° = 1260°.
Symmetry in a regular nonagon
A regular nonagon has 9 lines of symmetry and a rotational symmetry of order 9, meaning that it can be rotated in such a way that it will look the same as the original shape 9 times in 360°.
| Lines of symmetry | Rotational symmetry |
|---|---|
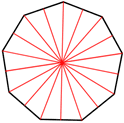 |
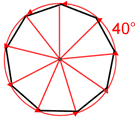 |
| 9 lines of symmetry | Nine 40° of rotation about the center. |
