Symmetry

In geometry, symmetry describes the balance a figure has. A figure or object has symmetry if a transformation(s) maps it back onto itself. Both plane and space figures may have symmetry.

There are three basic types of symmetry: reflection, rotation, and point symmetry.

Reflection symmetry

In Geometry, a figure can have reflection symmetry when it is reflected across a line or a plane.

Line symmetry

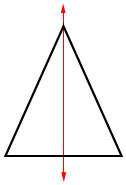
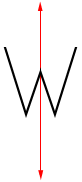
A figure has line symmetry if it can be reflected across a line back onto itself.

An isosceles triangle has one line of symmetry from its vertex to the midpoint of the base.		The letter W has one line of symmetry through its middle.

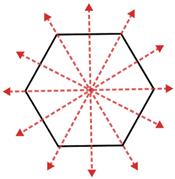
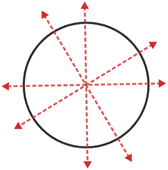
A figure can have multiple lines of symmetry.

A regular hexagon has 6 lines of symmetry.		Any line through a circle's center is a line of symmetry.

Mirror images

Any line of symmetry divides a figure into two mirror images. Folding half of the figure across the line of symmetry produces the other half of the figure.

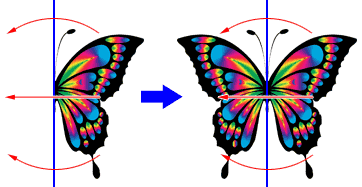
The right half of a butterfly is folded across the vertical line, shown in black above, to complete the drawing of the butterfly.

Translations that preserve distance

Whenever you reflect a figure across a line of symmetry, each point on the figure is translated an equal distance across the line of symmetry in the opposite direction, back on to the figure.

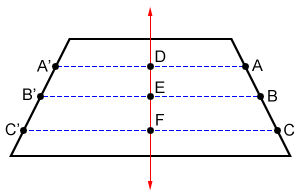
Points A, B, and C on the isosceles trapezoid above are translated across line DF to points A', B', and C'. The distance from each point shown on the trapezoid to the line of symmetry is equal to the distance from the reflected point to the line of symmetry; the distance from A to D is equal to that from A' to D. This must be true for all points on the trapezoid for it to exhibit symmetry.

Plane of symmetry

A plane of symmetry is a plane that cuts a 3D figure into equal halves such that the reflection of half of the object across the plane is the mirror image of the other half.

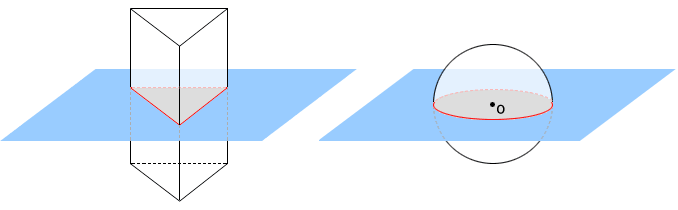
Geometric solids can have multiple planes of symmetry. For example, the rectangular prism below has three planes of symmetry.

Rotational symmetry

A figure has rotational symmetry if rotating it about its center at a given angle maps the figure back onto itself. The center of rotation is a point called the center of symmetry.

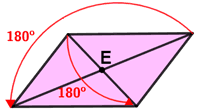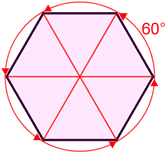
Rotating the parallelogram 180° about its center maps the parallelogram back onto itself.		Rotating the regular hexagon 60° about its center maps the hexagon back onto itself.

A space figure, such as a wheel, has rotational symmetry if the shape of the figure moves onto itself when rotated less than a full turn around a line.

Order of rotational symmetry

The order of rotational symmetry of a figure is the number of times you can rotate the figure within 360° such that it looks the same as the original figure. To find the order of symmetry, divide 360° by the smallest angle you can rotate the figure by to produce the original figure.

An order of symmetry of one means that there is no rotational symmetry.

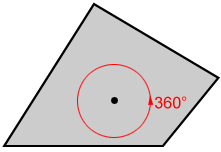
The order of rotation for the quadrilateral above is one. It takes a full rotation for the image of the quadrilateral to map on to itself, so 360° ÷ 360° = 1.

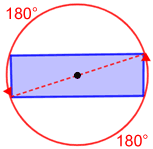
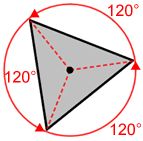
The following are some examples of rotational symmetry of order 2 or more.

Order 2	Order 3	Order 4

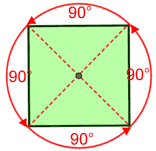Point symmetry

A figure has point symmetry if it can be reflected across a point back on to itself.

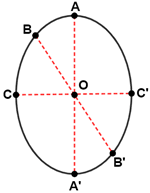
The ellipse above has its center at point O. Three points A, B, and C are reflected across point O to points A', B', and C' which are also on the ellipse and are the same distance from point O as their counterparts.

A plane figure that has point symmetry also has rotational symmetry of order 2 or more.

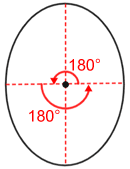
We can rotate the ellipse 180° twice to produce the original ellipse, so the order of rotational symmetry of the ellipse is 2.

The center points shown in red for the figures above are all points of symmetry.

There are many other types of symmetry aside from those described above, including translation symmetry and scaling symmetry.