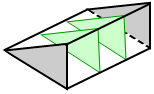
Triangular prism
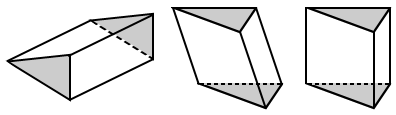
A triangular prism is a prism with triangular bases. The figure below shows three types of triangular prisms.
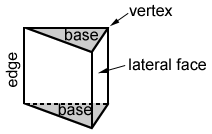
What is a triangular prism
A triangular prism is a 3D shape, specifically a polyhedron, that is made up of 2 triangles and 3 lateral faces. The triangles are congruent and are referred to as the bases of the triangular prism. The 3 lateral faces are also congruent and can be rectangles, parallelograms, or squares depending on the type of triangular prism. The figure below shows a triangular prism labeled with its respective parts.
Triangular prism net
The figure below shows a net of a triangular prism. The net of a 3D figure is what the figure would look like if opened out and laid flat:

Note that this is just one net of a triangular prism. A triangular prism has 9 distinct nets.
Properties of a triangular prism
- Number of faces: 5
- Bases (triangular): 2
- Lateral faces (rectangles / parallelograms): 3
- Number of edges: 9
- Number of vertices: 6
- All lateral faces are congruent; all bases are congruent
- Any cross section of the triangular prism that is parallel to the bases will yield a triangle that is congruent to the bases.
Triangular prism formulas
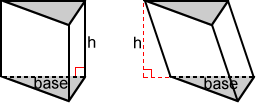
Volume of a triangular prism
The volume, V, of a triangular prism is the area of one of its bases times its height:
V = B·h
where B is the area of a triangular base and h is the height (the distance between the two parallel bases) of the triangular prism.
Surface area of a triangular prism
The surface area of a triangular prism is the sum of the areas of its 3 lateral faces and 2 bases and is given by the formula,
where SA is surface area, a, b and c are the lengths of the sides of the bases, b is the bottom side of the base, and h is the height of the base.
Types of triangular prisms
There are a few different types of triangular prisms such as regular and irregular triangular prisms, right triangular prisms, oblique triangular prisms, and more.
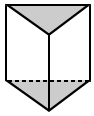
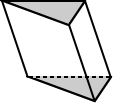
Regular and irregular triangular prisms
Triangular prisms can also be classified based on the type of triangle that forms its base. A regular prism is defined by a prism whose bases are regular polygons. Therefore, if the bases of the triangular prism are equilateral triangles, it is a regular triangular prism. Otherwise it is irregular. Often, a regular triangular prism is implied to be a right triangular prism.
| Regular triangular prism | Irregular triangular prism |
|---|---|
 |
 |
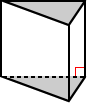
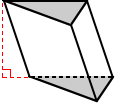
Right and oblique triangular prisms
Triangular prisms can be classified based on how their bases and lateral faces intersect or meet. If the bases are perpendicular to the lateral faces, meaning they meet at right angles, it is a right triangular prism. Otherwise it is an oblique triangular prism.
| Right triangular prism | Oblique triangular prism |
|---|---|
 |
 |