Octahedron

An octahedron is a space figure with 8 faces that are polygons. In the figure below are 3 different types of octahedrons. The prefix "octa" means eight.

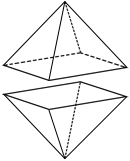
An octahedron can be formed by two pyramids with bases in the shape of a quadrilateral, as shown in the figure below.

Properties of a regular octahedron

A regular octahedron is an octahedron whose faces are all congruent, regular polygons. Otherwise, it is irregular. Regular octahedrons are studied more often.

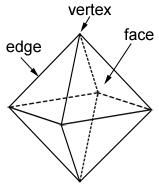
A regular octahedron, such as the one shown above, is one of the 5 Platonic solids, which are a type of regular polyhedron. A regular octahedron has 8 congruent faces that are congruent equilateral triangles, 12 congruent edges, and 6 vertices; an edge is a line segment formed by the intersection of two adjacent faces; a vertex for a regular octahedron is a point where 4 edges meet.

Surface area of a regular octahedron

We can find the area of one of the faces and multiply it by eight to find the total surface area of a regular octahedron. An equilateral triangle with side length, e (also the length of the edges of a regular octahedron), has an area, A, of

The total surface area, S, of a regular octahedron in terms of its edges, e, is,

Volume of a regular octahedron

The volume, V, of a regular octahedron is

where e is the length of the edge.